 統計学
統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤差が出ているからです。
例えばサイコロを300振って、1が60回出ました。これは1が出やすいサイコロだと言えるでしょうか。1~6までの各目が均等に出れば確率は1/6です。300回振れば、50回1の目が出れば1/6となります。しかし実際は均等に振っていてもばらつきが生じます。
上の例のように60回1の目が出ていてもばらつきの範囲内と言えるでしょうか。この様なケースには多々遭遇するのでは無いかと思います。歩留り改善対策を実施した結果、先月より0.3%上昇しました。果たしてこれは改善したと断言して良いのでしょうか。断言は出来ないけど悪化してないので継続してみましょうか、となりそうです。 逆に0.3%のダウンなら・・・効果なさそうなので止めましょう、となるかもしれません。
これが1%アップなら『効果ありました』と自信を持って言えるのか・・・。今回のようなケースはカイ二乗検定を用いて有意差と言えるのか、誤差程度なのかのを判定をする事が出来ます。
ある会社の先月の製造歩留まりが、96.7%でした。歩留まりを改善する為ある対策を実施した所、歩留まりは97.0%になりました。数値上は0.3%上がっていますが果たして改善したと言っても良いでしょうか(図1)
図1.製造歩留まりの推移
有意水準1%でカイ二乗検定を行うと73%の確率で、この程度の差異は生じ得ると言う判定結果となります。 つまり統計的には改善されたとは見なされない結果となります。まさに誤差範囲での変動を効果があると喜ぶ『 悲劇 』が生じるのです。統計的手法を用いれば、数値の変化に一喜一憂する前に、果たしてそれが意味がある変化なのかどうか、判断することが可能になります。
上の例は歩留まりですが、約1000人採用した場合の一年後離職者数として考えれば、採用の 評価でも同じように活用することが出来ます。決して製造業向けの方法では無く、あらゆる業種・職種で用いることが出来ます。ビジネスシーンでは、アクションに対する効果有無の比較は当たり前の様に行われていて、数値の比較が行われいるケースは、製造業に限らず多々あると思います。
...
 統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤差が出ているからです。
統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤差が出ているからです。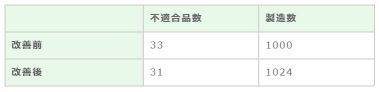

 統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤差が出ているからです。
統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤差が出ているからです。
 統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤差が出ているからです。
統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤差が出ているからです。