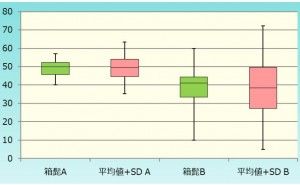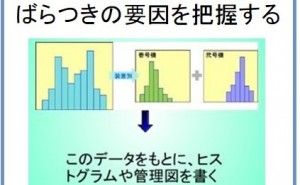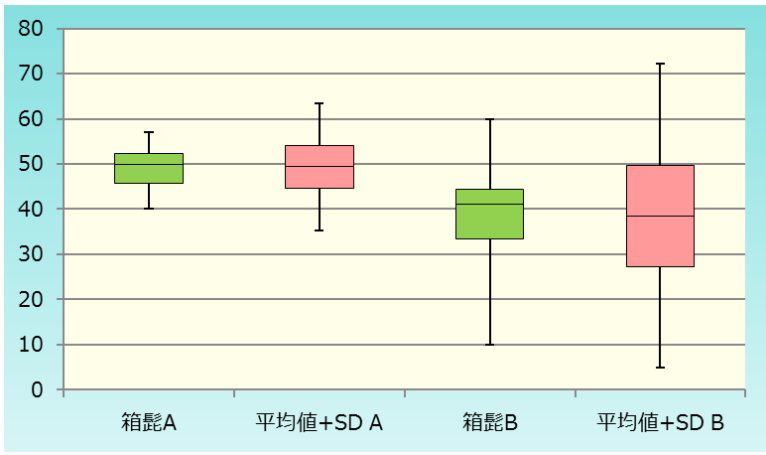
層別比較に便利なグラフ


続きを読むには・・・
この記事の著者

この記事の著者
眞名子 和義
ムダ・ムラ・ムリの「3ムの撤廃が企業収益向上に繋がる」を信条とし、お客様の"視座"に立ったご提案を致します
ムダ・ムラ・ムリの「3ムの撤廃が企業収益向上に繋がる」を信条とし、お客様の"視座"に立ったご提案を致します
「SQC一般」の他のキーワード解説記事
もっと見る統計手法の中の『層別』とは
今回は、統計手法の中の層別という分析手法について、解説します。 層別の基本的意味について整理してみますと、一般の方で...
今回は、統計手法の中の層別という分析手法について、解説します。 層別の基本的意味について整理してみますと、一般の方で...
「微分」 現場数学(その1)
♦ 数学の教科書に書いてある通りにプログラムしてもだめ!では計算できない! サイン・コサイン何になる…とか嘯(うそぶ)い...
♦ 数学の教科書に書いてある通りにプログラムしてもだめ!では計算できない! サイン・コサイン何になる…とか嘯(うそぶ)い...
~スパコンは速くなった? 続・現場数学(その19)
1. 新幹線とスパコン“速さ”の違い 東北新幹線は最高時速260kmで走っていました。それが、...
1. 新幹線とスパコン“速さ”の違い 東北新幹線は最高時速260kmで走っていました。それが、...
「SQC一般」の活用事例
もっと見るビックデータ時代と米国大統領戦
ビックデータ時代を考える事例として、今回の第45代米国大統領選挙を見てみます。第45代の米国大統領に、ドナルド・トランプ氏が決まりましたが、トランプ氏当...
ビックデータ時代を考える事例として、今回の第45代米国大統領選挙を見てみます。第45代の米国大統領に、ドナルド・トランプ氏が決まりましたが、トランプ氏当...
第1種の誤りと第2種の誤り
「あわて者の誤り」と「ぼんやり者の誤り」をご存知ですか、あわて者の誤りは正式には『第一種の誤り』(Type Ⅰ error)と呼称し、ぼんやり者の誤りは...
「あわて者の誤り」と「ぼんやり者の誤り」をご存知ですか、あわて者の誤りは正式には『第一種の誤り』(Type Ⅰ error)と呼称し、ぼんやり者の誤りは...
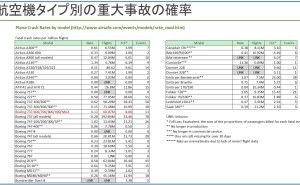
飛行機事故とセンサー・フィードバックの分布
ボーイング 737 Max 8機が短い期間に2回の墜落死亡事故を起こし、多くの航空会社が同機種の運航を停止する事態となっています。多くの...
ボーイング 737 Max 8機が短い期間に2回の墜落死亡事故を起こし、多くの航空会社が同機種の運航を停止する事態となっています。多くの...