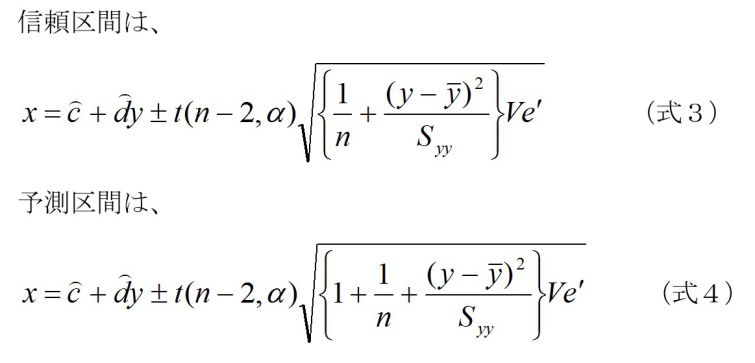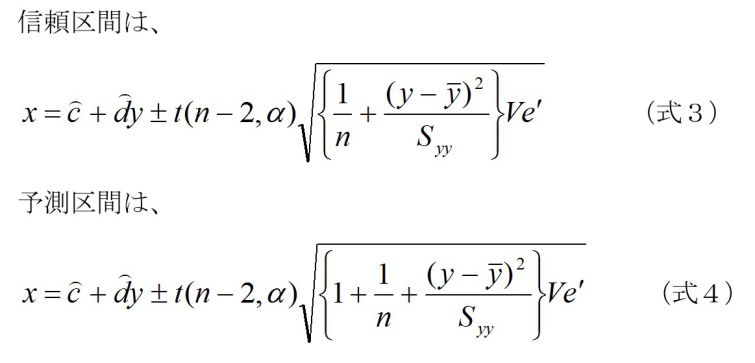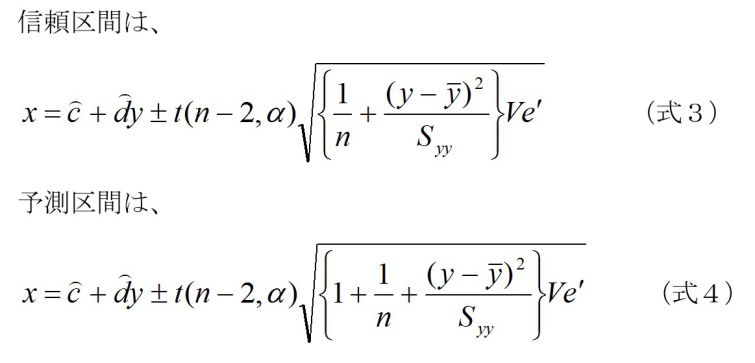母体から、20個とか50個をサンプリングしてきてその平均をとった場合、母体の真の平均からずれますが、どの程度ずれているのかがわかれば非常にアクションがとりやすくなります。リスクマネジメントしやすいということです。ズレ幅の計算により、予想値が小さいときには投資しないとか、その逆なら投資しようとかの判断にも使えます。
この計算は、信頼区間からできます。又、計算方法は若干違いますが、単回帰分析における直線の式に関しても通じます。信頼区間というのは、点推定(標本平均)に対して、信頼水準を設定した後で計算する、いわば、ばらつく範囲の予想みたいなものです。さらに、信頼水準とは、有意水準αとして、(1-α)としたもので、95%あたりがよく使われます。この辺の厳密な話は別にして、95%とれば、大抵のことは推定できます。信頼区間は、回帰式±信頼区間幅 で、実際の計算は下記のようになります。
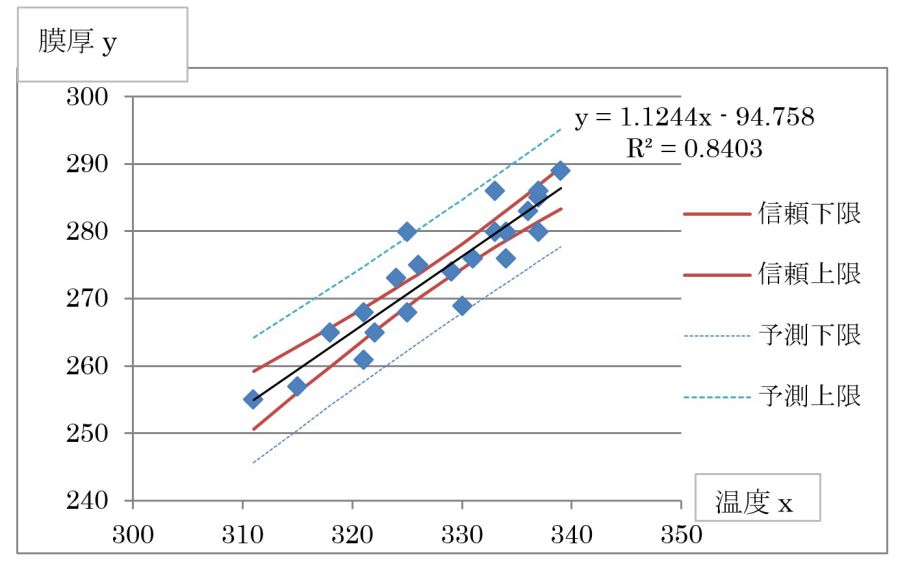
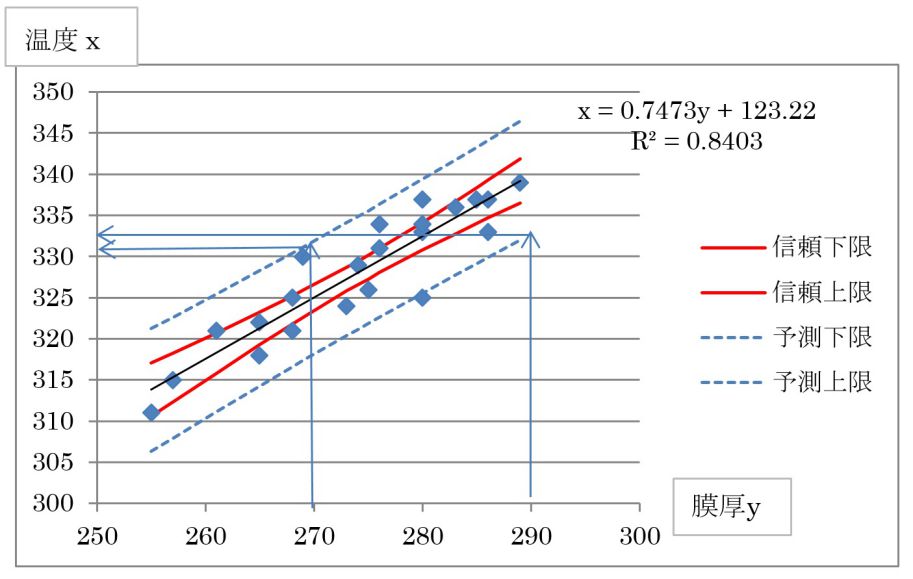
今、あるデータの(x、y)を上記計算で図1のようになったとします。
図1. 温度xに対する膜厚の出来栄え (n=20)
図1は、温度xがいくらの時に膜厚yがどの程度ばらつくか、ということです。通常は、信頼区間よりは予測区間に関心があるので、図1の青点線がその範囲になります。温度が320℃なら、膜厚yは258から275までばらつくといった予測になります。この範囲に95%が入ってくるということです。(100回実験すれば95回はここへ入る)
膜厚の上限が280ぐらいなら問題ないが270であれば、不適合が発生する可能性大です。そういう見方をすれば、このデータしかない場合のリスク管理がしやすくなります。それでは、膜厚の規格が決まっている場合、逆に温度は何度である必要があるでしょうか? 膜厚の規格を270から290として考えてみましょう。
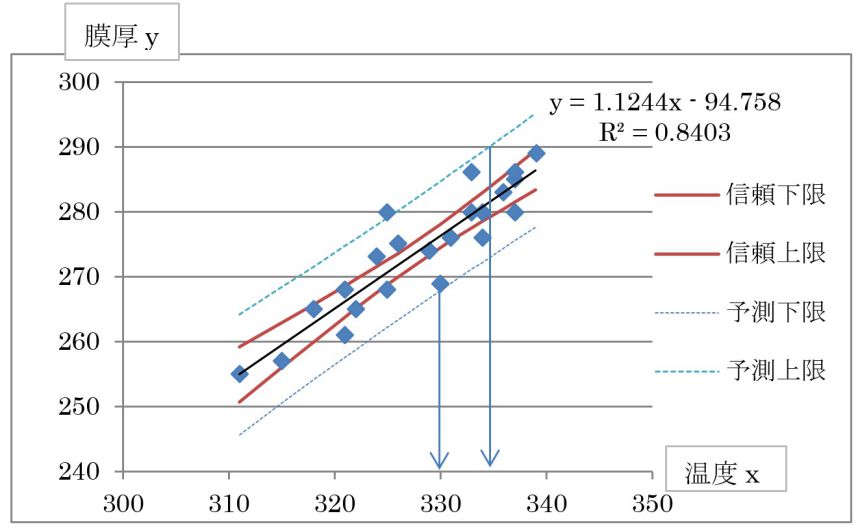
図2. 出来栄え規格から原因系規格を設定の例(誤用)
図2では、予測の上下限を使って、区間推定から原因系の温度範囲を求めています。その結果、330℃から335℃になります。(図2の矢印値を読む) 一見正しそうですが、よくある誤用です。回帰は、xからみたときのyのばらつきを解析しているので、yからみたときのxのばらつきを考慮していません。yからみて、xがどうなるのかは、グラフの縦横を入れ替えて考えないといけません。(逆推定という)これは、センタ―ラインである回帰直線についても同様のことです。xとyを入れ替えるだけなので、計算は同様ですが、解析結果は変わります。式は、下記のようになります。
図示すると、
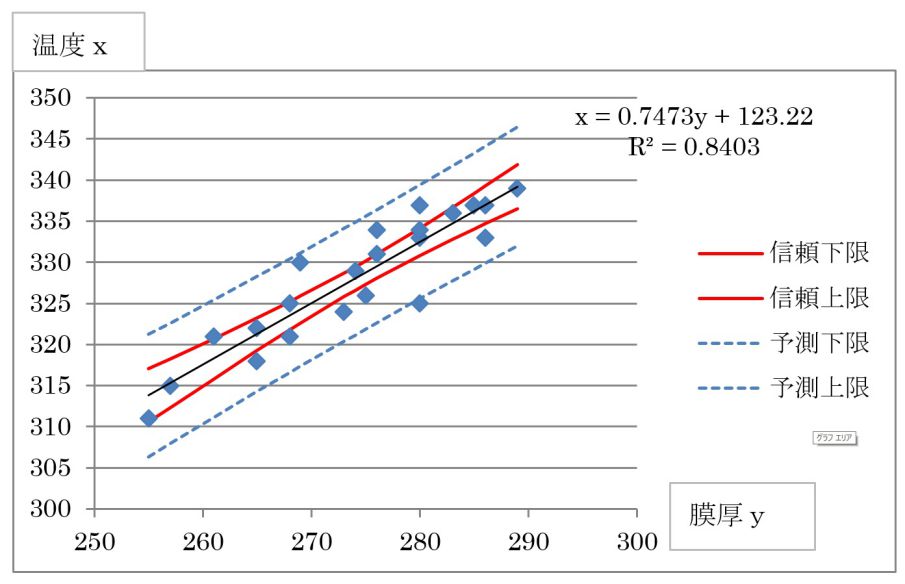
図3. 膜厚yに対する温度xの区間推定
図4. 膜厚規格から温度範囲を設定する図
図4から、膜厚を270~290にしたいなら、温度は331℃から332℃にコントロールが必要となります。図2から読み取った場合は、330℃から335℃でしたから、温度制御範囲幅は5度から1度に変わります。量産での投資設備はこれを満たすものでなければいけませんし、既存装置で製造なら不適合発生率を推定しコスト対応しないといけません。傾きが1でない場合や、平均付近から離れた場合の推定の場合、コントロール範囲が解析方法で大きく変わります。注意が必要です。
・補足1.
x(横軸)からy(縦軸)の普通の回帰式は、図1、図2の右上に記載されていますが、y=1.1244x-94.758 です。これをxについて解くと、x=0.8894y+84.274 (式3)となります。あきらかに、逆推定の場合の式 x=0.7473y+123.220 と異なっています。信頼区間もこれにつれて異なったものとなります。
・補足2.
x(横軸)には原因系を、y(縦軸)には結果系をというのが基本であって、このため、横軸変数に対する回帰を考えているので、これを入れ替えて考えるのはおかしいという考え方もあります...