【統計手法による 2018年LPGA公式記録データの解析 連載目次】
1. 相関・主成分・クラスター・レーダーチャート分析の事例とは
2018年の国内女子ゴルフツアー(LPGA)は終了し、アンソンジュが年間獲得賞金女王となりました。LPGAから女子プロゴルファー上位95名の公式記録データが報告されています。今回は、このデータを使って、プレーの実力を決めるための技能(以下変数、各変数の定義は末尾の注を参照ください)、選手の特徴等を「相関」「主成分「クラスター」「レーダーチャート」分析の事例として整理して解説します。なお、この手法は「事業戦略」「マーケティング」等にも使われている有効な手法です。1)2)3)
2. 解析の前提条件
獲得賞金額はツアーによって賞金額が異なるため、変数から外し、技能面に着目した解析としました。前提条件は次のとおりです。2018年女子プロ上位95名の公式記録データを使用し、年間の平均ストローク数他9項目の成績を対象としました。
成績の大きさを一致させるために、平均ストローク(=72-実績平均値)、平均(2-実績平均値)としました。各説明変数は標準偏差(σ)で基準化したデータに変換しました。
解析は「相関分析」「主成分分析」「クラスター分析」「レーダーチャート」とし、変数の特性と選手の特徴を浮き彫りにします。
3. 記録データの加工
表1にLPGA公式記録データ95選手の内、上位3選手の成績を示します。
表1.LPGA公式記録データ(平均ストローク上位3位)
表2は上記各変数を標準偏差(σ)で基準化した数値です。((μ-x)/σ)μ;各変数の平均値、 x;変数
表2.記録データの標準化
4. 記録データの相関分析
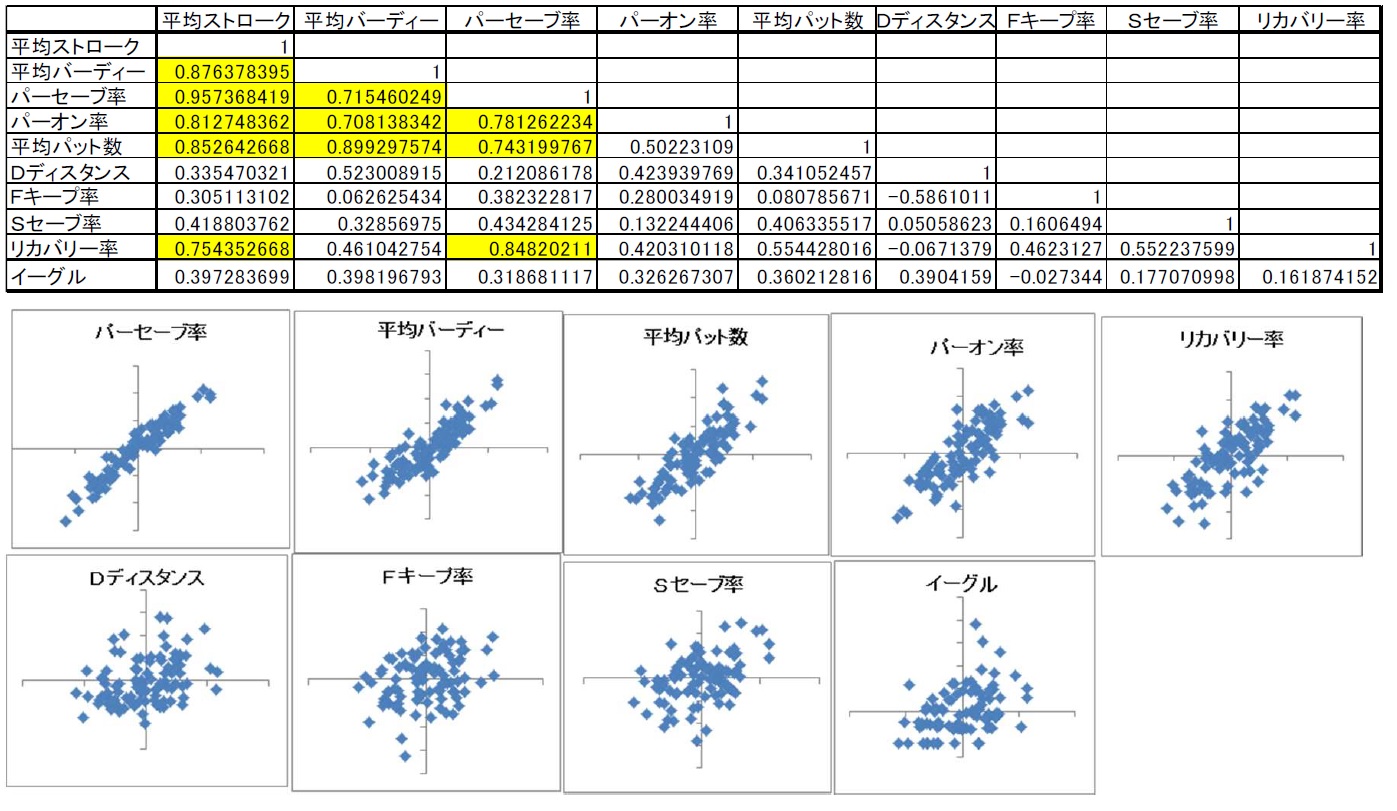
10変数の相関係数を計算した結果を表3に示します。それの散布図を図1に示します。
平均ストロークと大きな相関があるのは「パーセーブ率」「平均バーディー」「平均パット数」「パーオン率」「リカバリー率」になります。これを仮に「5つの変数」と呼びます。
一方、「Dディスタンス」「Fキープ率」「Sキープ率」「イーグル数」は平均ストロークと無相関であることが表3、図1から分かります。ゴルフゲームを複雑にしているのは、この「5つの変数」間で発生する「交互作用」すなわち多重共線性(マルチコ)を有することです。
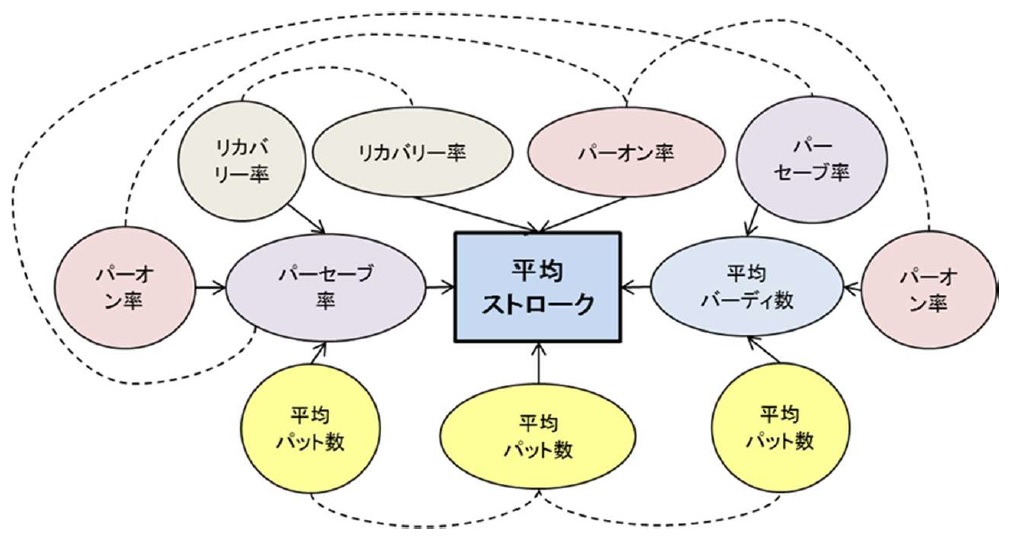
例えば、平均パット数は「5つの変数」の一つですが、図2の「平均ストロークと他変数の相関図」をみると「5つの変数」のパーセーブ率、平均バーディー数にも影響を与えていることが分かります。同様に「多重共線性」はパーセーブ率、リカバリー率にもみられます。
「多重共線性」を有する系は、線形回帰分析は不可能であり、非線形回帰で分析することになりますが、複雑化するため、ここでは「主成分分析」等を使って解析していきます。
参考ですが野球はホームラン、盗塁、三振、安打は独立性の高い変数です。しかし、ゴルフは説明変数のいくつかは「交互作用」を有することに大きな相違があり、野球は比較的簡単な線形回帰式で解析できることが特徴です。
表3.10変数の相関係数行列
図1.平均ストロークとその他変数の散布図
図2.平均ストロークと他変数の相関図
次回に続きます。
【注】
- パーオン率;パーオンをする率
- バーディー数;1ラウンド当たりの平均バーディー数
- パーオン率;パーオンしたホールの平均パット数
- Dディスタンス;ティーショットの平均飛距離
- リカバリー率;パーオンしないホールでパーかそれより良いスコアを獲得する率
- イーグル数;イーグルの年...