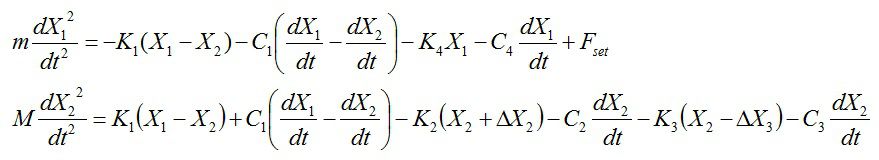1.パラメータ設計の極意は「無用の用」―システムは複雑でなければ改善できない―
パラメータ設計においては、「システムは複雑でなければ改善できない」と言われています。 これは荘子が唱えた「無用の用」に通ずるものがあります。 中国の孔子のような崇高な理念の持ち主とは対照的な人物に老子や荘子がいますが、孔子を人生の「ユークリッド哲学」とすれば、価値観の座標が現実把握を重視した「非ユークリッド的」な発想の持ち主が老子や荘子です。荘子が唱えた「無用の用」は、空のところが役に立つと考えました。 「有るもの」に対して「無いこと」に価値を認めた考えが無用の用です。 道幅も足の幅だけでは自由に歩けないように、パラメータ設計でもたくさんの無駄と思われる制御因子による「非線形効果」のおかげで、ノイズに強い安定化設計が可能になるのです。 現在の変化の激しい世の中では,世の中が濁っていたらいっしょになって泥水を跳ね返すことが必要であり、融通無碍に行動することが大切です。
パラメータ設計の特徴である「非線形効果」の利用とは次のような意味をもちます。 まず初めに制御因子とノイズとの交互作用(善玉)でノイズの影響に強い制御因子を選んで「ロバストネスの研究」を行い、その後で制御因子の「線形効果」を利用して、目標値へ合わせ込む「2段階設計」を行うのです。 「再現性」のチェックは「直交表」で、「安定性」のチェックは「SN比」で行います。
2.「無用の用」の具体事例(その1)発振回路
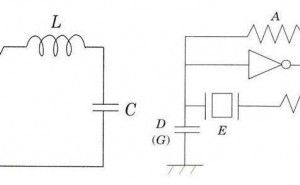
田口博士が「システムが複雑でなければ改善はできない」と提唱し、パラメータ設計の制御因子は沢山必要であることを力説したのも奇想天外の着想といえます。 図1に示す回路はLC発振回路で、制御因子は電源回路、抵抗、インダクタンス、キャパシタンスの4個しかありません。
一方図2に示す回路はセラミック発振回路で、機能は同じですが制御因子はやや複雑です。
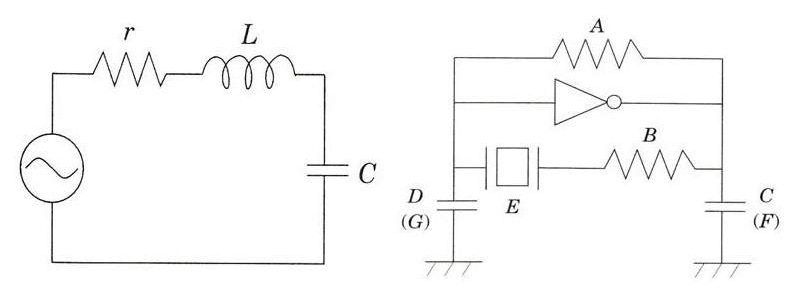 図1.LC発振回路 図2.セラミック発振回路
図1.LC発振回路 図2.セラミック発振回路
さらに図3に示す回路はトランジスタ発振回路であり、図1や図2に比べてはるかに複雑な回路で、制御因子は数十個以上あります。
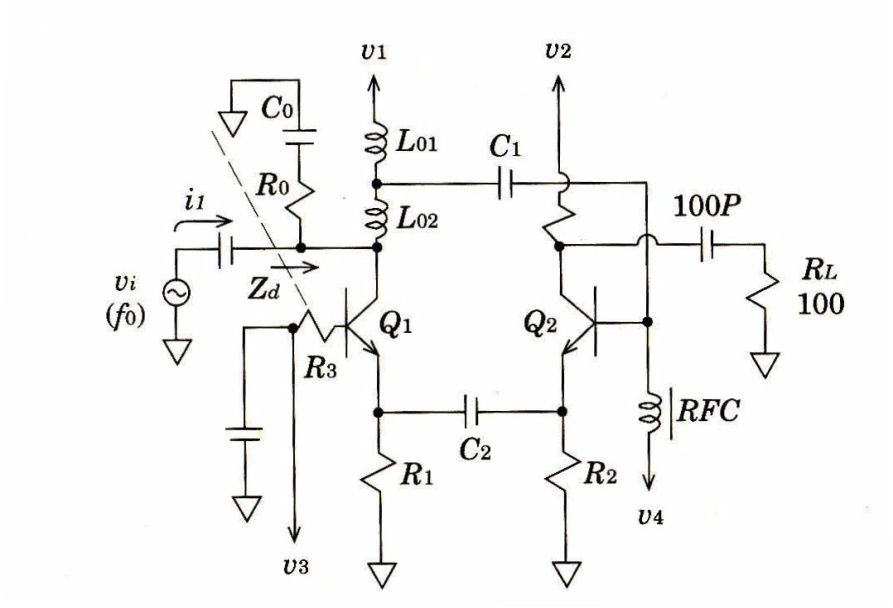
図3.トランジスタ発振回路
システムは合理的だが複雑なものがよく、システム選択の難しさはそこにあるのです。 同じ機能でも単純なものは制御因子が少ないので、機能性の高い設計が難しいわけです。(安定性・再現性)
3.「無用の用」の具体事例(その2)プランジャー
3.1 信頼性試験でトラブル発生
デイジープリンターを開発したとき、電磁石のプランジャーが内部から発生する熱で「2度打ち」を起こす現象が発生しました。 原因は、プランジャーが衝突するゴムの緩衝体が温度上昇で硬化するという現象です。 バウンド量規格が0.5mm以内に対して最大2.5mmまで上昇しました。
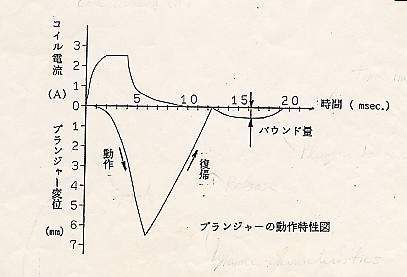

図4 プランジャーの動作特性図
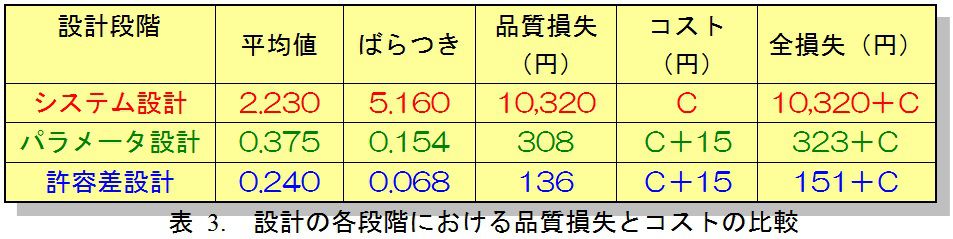
3.2 システム設計とパラメータ設計
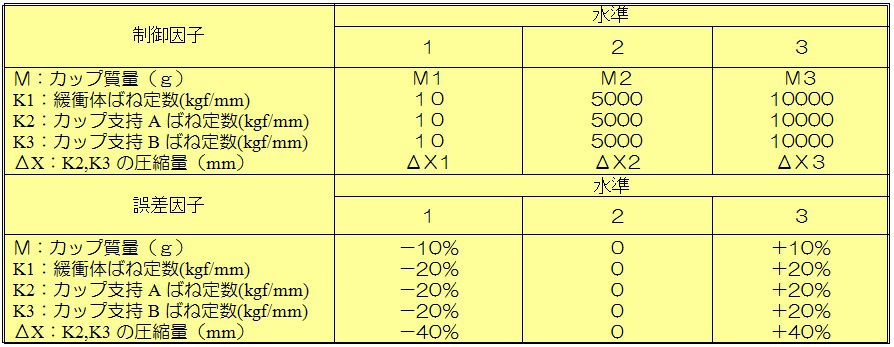
品質工学とコンピュータシミュレーションを活用して、プランジャーの衝突前後のマクスウェル運動方程式を使って、パラメータ設計を行った結果、温度変化のノイズに強いシステムを考案することに成功しました。
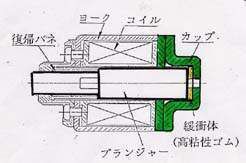
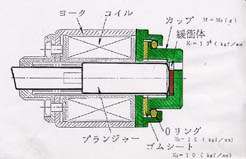
図5 システム設計の構造図 図6 パラメータ設計の構造図
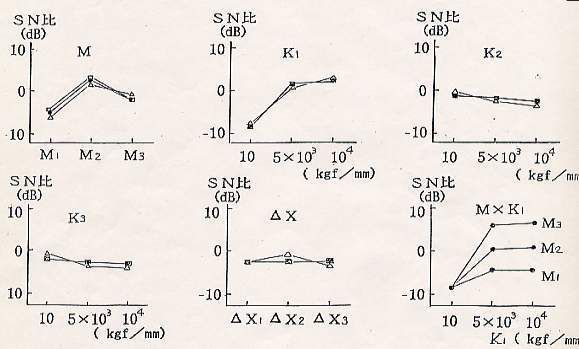
パラメータ設計において、ノイズと多くの制御因子との交互作用による非線形効果によって、温度などのノイズの影響に強い制御因子の水準が見つかったのです。 最初のシステム設計では図5のような単純な構造であったため、図7に示すように電磁石自体の温度上昇でプランジャーの2度打ち現象が発生して、バウンド量が,許容差を遥かに越える状態が起きていました。 システム選択の段階ではCAEを活用して、複雑なシステムを考案する重要性が分かります。
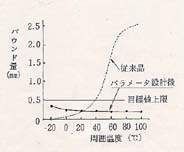 図7 周囲温度とバウンド量の関係
図7 周囲温度とバウンド量の関係
そこでこの問題を解決するために、図8のようなシミュレーションモデルの等価回路を考えて、プランジャーが衝突する前と衝突後のマックスウェルの運動方程式をつくり、パラメータ設計を行いました。
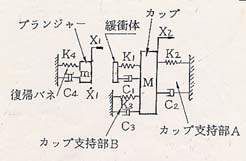 図8 シミュレーションモデル
図8 シミュレーションモデル
M:カップの慣性質量 K1:緩衝体の等価ばね定数
C1:緩衝体の等価粘性係数 K2:カップ支持部Aの等価ばね定数
C2:カップ支持部Aの等価粘性係数 K3:カップ支持部Bの等価ばね定数
C3:カップ支持部Bの等価粘性係数 m :プランジャーの慣性質量
K4:復帰ばねの等価ばね定数 C4:復帰ばねの等価粘性係数
ΔXi:K2 ,K3 の圧縮量
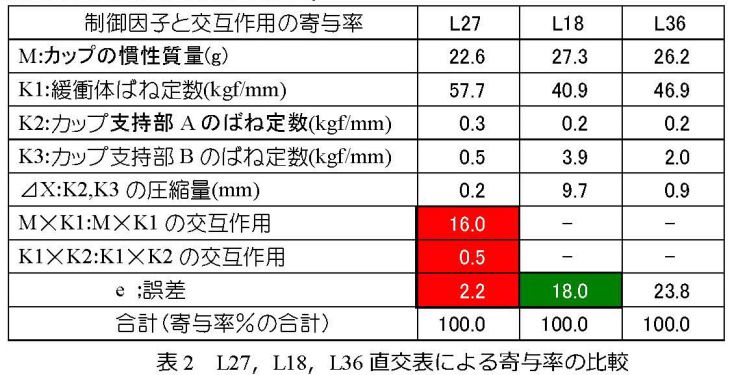
■ プランジャーが緩衝体に衝突する前後の運動方程式を使って、「バウンド量」を「ゼロ望目特性(バウンド量X1=±0)」として解析しました。 ゼロ望目特性のSN比は、以下のようにな...