１．はじめに：実験計画法と応答曲面法

　本稿は2016年に統計的品質管理（Statistical Process Control: SQC）手法の１つである実験計画法（Design of Experiment: DOE）の活用についてご説明した内容の続編です。当時の説明図を一部修正して図1から図3に再掲します。図4は今回新たに追加したものです。 前稿ではまず初めに、2つの量的因子 x₁,x₂ について多水準、特に x₁を重視するため x₁は5水準、x₂は4水準として図1の実験領域を持つ全15回の「我流」でアンバランスな要因配置計画を採用したことをご説明しました。しかし得られたデータから有意義な解析結果を得ることができなかったことから、全16回の「SQC手法」に基づく二元配置計画を図2のように提案しました。x₁の水準数を減らしても確実な結果が得られるバランスのとれた保守的な計画を推奨しました。さらに量的な3因子であれば全15回の中心複合計画（Central Composite Design: CCD）を採用することで多水準の効果を効率的に評価できることを紹介しました。このCCDが本稿のテーマである応答曲面法の1つです。

２．応答曲面法とは

　CCDに代表される応答曲面法（Response Surface Methodology: RSM）の概要を以下に説明します。RSMとは、応答（実験結果）y を因子x₁,x₁,… x_p（pは整数）の2次の推定式で表すために必要な実験の計画と、その実験結果を解析するための方法論です。本稿では p=3 とします。2次の推定式を具体的に表すと式（1）となります。このとき関数 f（x₁,x₂,x₃ ）を応答曲面関数、2次式は2次モデル（second order model）と呼びます。ε は因子に依存しない純粋な実験誤差で純誤差（pure error）と呼びます。

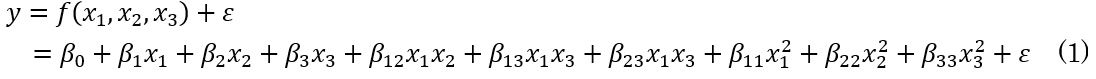
　2次モデルは応答 y を曲線（曲面）として解析することから、式（1）を前提とした実験計画法を応答曲面法と呼びます。2次項の係数 β₁₁,β₂₂,β₃₃は2次の効果（second order effect）の大きさを表しています。この大きさが純誤差 ε と比較して有意に大きければ2次の効果があり、そうでなければ2次の効果はないと判断します。効果がない場合は2次項の係数は0となります。このとき、2次項が欠けることによる式（1）と実際の応答との乖離の評価、すなわちあてはまりの悪さ（Lack of Fit: LOF）を評価することがあります。LOFの説明は紙面の都合で割愛します。

３．応答曲面法のポイント：計画時

　RSMの実験を計画する時のポイントは次の3つです。第1は因子が量的であること、第2は因子の水準は3水準以上に設定すること、第3は純誤差を評価するため実験の繰返しを行うことです。RSMの代表的な計画としてCCD及びBox-Behnken Design（BBD）があり3因子を例に説明します。

3.1　CCDの場合

　まず初めに3因子のCCDを図3で説明します。立方体の格子点（8点）、中心点を通る軸上点（6点）、中心点（繰返し数の点数）を実験点としています。8つの格子点から1次の効果と交互作用、6つの軸上点と中心点から2次の効果を推定し、中心点の繰返し（経験的に3～6回）から純誤差を推定します。このとき実験数は17～20回となります。各効果を評価する実験と中心点での繰返し実験を複合していることから中心複合計画と呼びます。
　CCDでは中心点から軸上点までの距離（αとする）もポイントとなります。立方体の1辺の長さは水準間隔を表し、第1水準を－1、第2水準を＋1とすると1辺の長さは2となります。このとき α=∜N=∜8=1.68 であれば、応答曲面関数 f（x₁,x₂,x₃ ） から計算される推定量の分散は、中心点からの距離が等しい実験点については同じ値となります。これを回転可能性（Rotatability）と呼びます。N は1次の効果と交互作用を推定するための実験の回数で本事例では N=8 です。

3.2　 BBDの場合

　次に3因子のBBDを図4で説明します。実験点は立方体の格子点ではなく、各辺の中点（12点）及び中心点（繰返し数）です。中心点の繰返しをCCDと同様に3～6回とすれば実験回数は15～18回となります。また、応答曲面関数 f（x₁,x₂,x₃ ）から計算される推定量の分散を評価することは可能ですが、中心点からの距離が等しい実験点について同じ値となるように実験を設計することはできません。よって回転可能性を評価することはできません。

3.3　CCDとBBDの比較

　CCDの利点は回転可能性があること、各因子の取り得る最大値及び最小値を全て組み合わせて実験点を設定できることです。欠点は各因子の設定が5水準と多いことです。回転可能性のある x₁,x₂,x₃ の規格化した実験点はそれぞれ  (-1.68, -1, 0, 1, 1.68)です。ここで、軸上点が示す実験条件 ±1.68 が日常設定している工程条件よりはるかに小さいまたは大きい場合、物理的に設定できない可能性があります。BBDの利点と欠点はこの逆となります。各因子の設定水準が3水準であることは、日常設定している工程条件をそのまま適用できる利点があります。一方、CCDより実験領域が狭くなることには十分注意が必要です。（x₁,x₂,x₃）=（1,1,1）の実験点をとることはできず、（x₁,x₂,x₃）=（1,1,0）,（1,0,1）,（0,1,1）で実験をしなければなりません。

４．応答曲面法のポイント：解析時

　RSMの実験結果を解析する時のポイントは、繰返し実験数や回転可能性を考慮したうえで解析するため難易度が高くなることです。現代ではPCやタブレットが普及しています。そこで計算そのものは統計解析ソフトウエアで実行することが現実的です。そうすれば解析結果の検証も容易で確実になります。そのうえで技術者は、コストパフォーマンスを考慮し戦略的な実験を計画（Plan）することが重要となります。そして実験の実施（Do）とデータの解析及び考察（Check）を行った後は、それに基づく対策の実施（Action）に専念すること、PDCAをしっかり回すことが大切です。

５．おわりに：戦略的な実験計画と応答曲面法

　実験の計画は、戦略的すなわち目的に合わせた実験を計画することが最も重要です。一般に実験の目的は2つあり、それは要因の絞込みと絞り込んだ要因による特性のモデル化であるとされています。まず初めにスクリーニング計画（Screening Design）を採用し、その後モデリング計画（Modeling Design）を採用します。前者は些細な多数（trivial many）の因子と極めて重要な少数（vital few）の因子をふるい分け（screening）するものです。後者はふるい分けされたvital few を実験因子として、少ない実験回数で正確に応答をモデル化する計画です。この方法論の1つがRSMです。そして、その具体的な計画がCCDでありBBDとなります。