【層別因子を含むデータ解析 連載目次】
♦ 重回帰分析初心者向けの注意 ～ 水準2個の場合
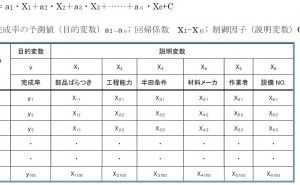
よく出てくるシチュエーションに、機械号機の差を含んだ重回帰分析や判別分析があります。以下の話は共通ですので、重回帰分析を例にします。重回帰分析の初歩レベルでのお話ですが、層別因子を含んだ例は、市販テキストにも載っていない場合が多いです。重回帰分析では、目的変数（従属変数ともいい、単に特性値ともいう）と説明変数（独立変数）から構成されています。目的変数をｙ（解析目的の収量であったり、寸法であったり、結果系、出来映え系のことです）とし、説明変数をｘi（iは、1，2，3，、、で、原因系。温度、圧力、触媒の量、とか。ｘ０と書いた場合は、重回帰分析の式の定数項）とします。
本来は目的変数も伴う誤差の仮定として、独立性、不偏性、等分散性、正規性が大事なため、通常は連続した計量値が望ましいわけです。この問題も結構あり、例えばアンケートの得点やキズの個数、収率などは、ひと工夫しないといけないわけですが、一旦差し置きまして今回は、説明変数のほうのお話をいたします。
説明変数にも、よく似た注意は必要です。例えば、濃度や温度は連続計量値ですが、層別因子は注意が必要となります。椅子の数（整数因子）などは、計量値ではないのですが、椅子の数1.６個が最適だとなれば、多めに2個配置しようという対策が取れます。つまり、計量値として解析しても大きな実害はないわけです。椅子の数（整数）に、小から大という順序関係、大小関係があるからです。ところが層別因子の場合、1号機と2号機はあっても、1.6号機というのは存在しません。ただし、1号機に１を、2号機に２を当てても、2台しかない場合は構いません。1号機に０を、2号機に１を当てても同じです。当然、回帰式は当てる数字によって異なりますが、その決定係数や回帰式の有意性が変わるわけではありません。また、回帰式が変わるといっても、定義した数値通りに打ち込めば、重回帰式から得られる予測値は一致します。例で示しましょう。次の事例は、多変量解析法（日科技連、奥野他）p123表7.8から抜き出して編集、改変したものです。
x1とx2は構成部品の部品寸法で、ｙは電気特性のようです。ここで、x3を機械号機とします。1号機と2号機のような感じです。1号機には１を、2号機には０という数字をあてがいます（この辺は先ほどの本とは異なる解説です。本から頂いたのは、データのみです）。ここで確認したいのは、1号機に１，2号機に２など、何を持ってきても解析結果が異なることがないということです（回帰係数は変わりますが、変数に定義された数字を入れれば、結果は一致します）。
表1. 各変数の説明（ｘは説明変数、ｙは目的変数）
表2. 対応させたデータ（連データ）（１）
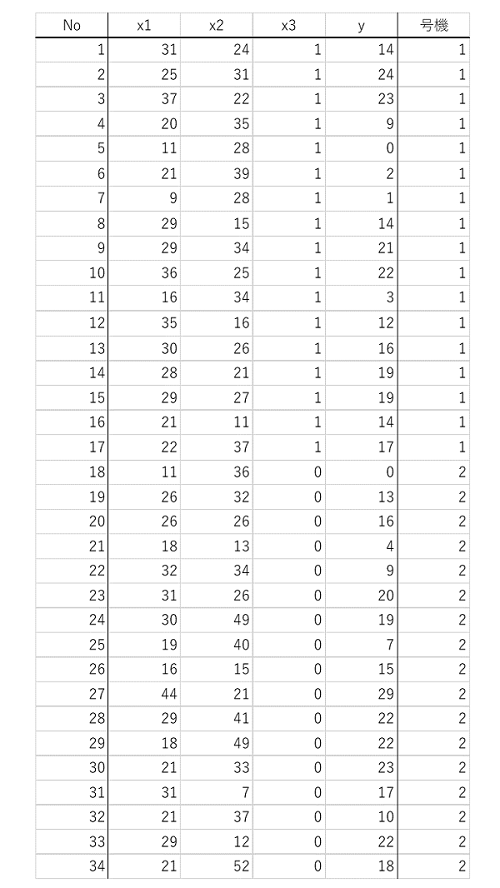
表3. 相関行列（１）
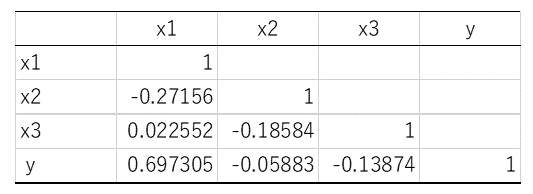
表4. 重回帰分析結果
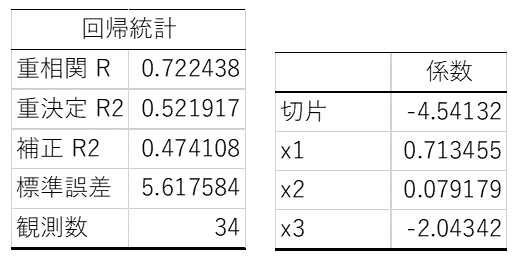
これは、回帰式Y＝-4.54132+0.713455x1+0.079179x2-2.04342x3 ということです。
このYを観測値（実現値）ｙと列記すると、
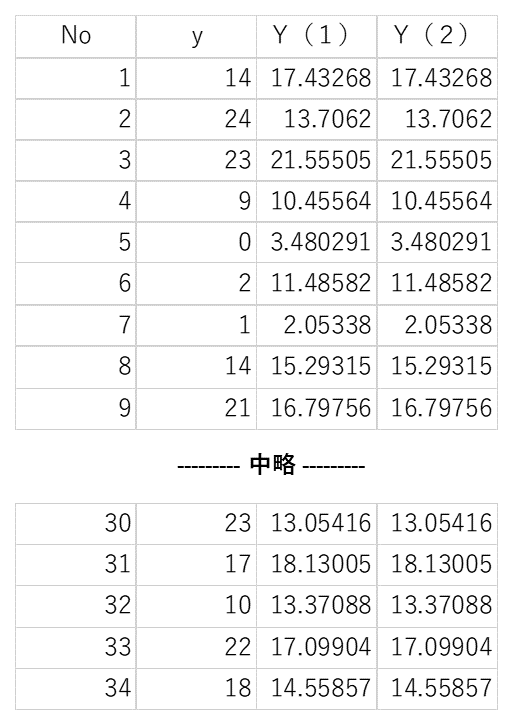
表5. 観測値と予測値（１）
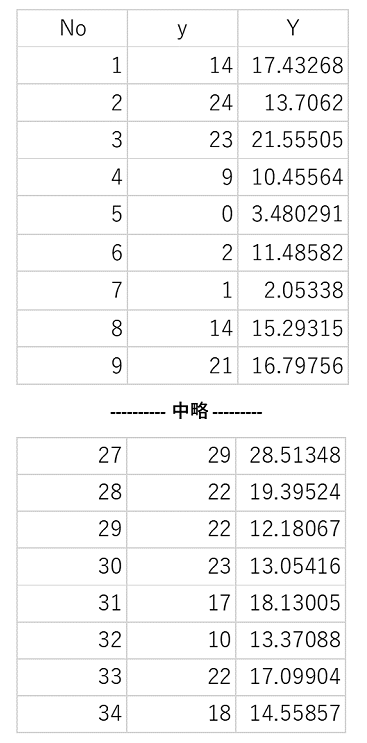
これが、機械号機1号機に１を、2号機に０を定義して割り当てたものの結果です。次に、機械号機1号に１を、2号機に２を割り当てて、同じことをやってみます。
対応データは下表のようになります。
表6. 対応させたデータ（連データ）（２）
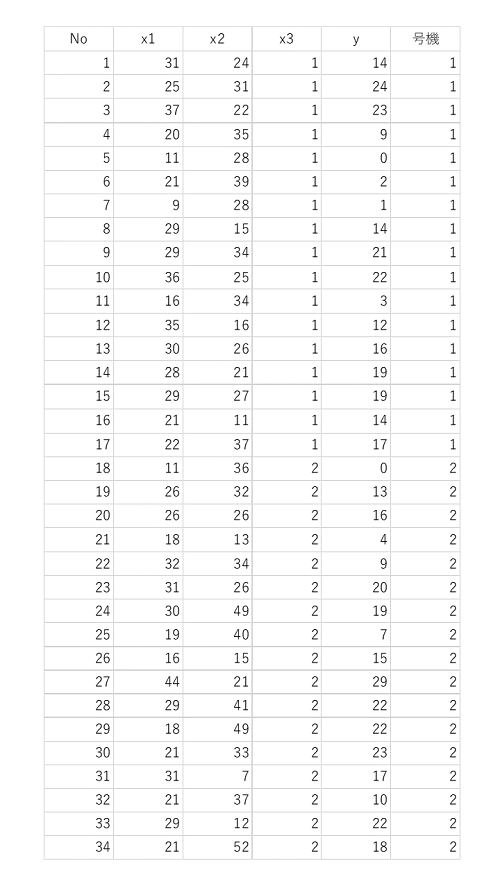
表7. 相関行列（２）
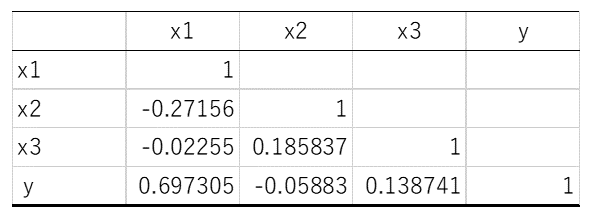
1号機に１を、2号機に０を定義したときの相関行列（１）とは正負が一致しませんが、大小を逆に定義したためです。大小関係を一致させておけば一致します。
表8. 重回帰分析結果（２）
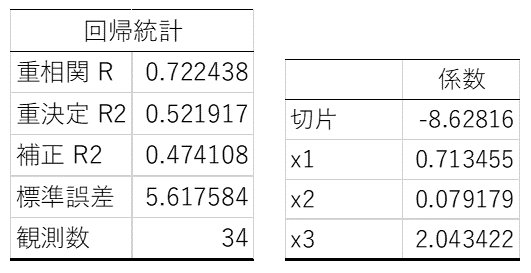
回帰統計は（１）と一致します。要は、定義変数を適当に変えても、寄与率や決定係数は変わりません。係数は一致しません（定数項も）が、この回帰式に定義した数値を当てはめてみると、得られる予測値Yは以下のようになり、...
表9. 観測値と予測値（１）と（２）
層別因子の水準が2個しかない時は、適当に2つの数値を割り当てればよいことになります。何でもいいわけです。決定係数は一致し、回帰から得られる予測値も一致します。相関行列や回帰係数は一致しませんが、もともと、物理的に意味のある数値ではないので、一致しなくても構いません。意味がないからです。要は、2個の水準値で比較するので、大小関係がひっくり返るだけのことです。また2個の水準ですから、その間の回帰は直線になるので、決定係数は個々の水準値に付随したｙのバラツキのみから決定されるため一致します。
ところが、機械号機の1号機、2号機、3号機に対し適当に、―１,０,１とか、１,２,３など割り当てることは厳禁です。
続きは次回解説記事（その2）で説明いたします。