1.回帰直線はyの残差を最小とする
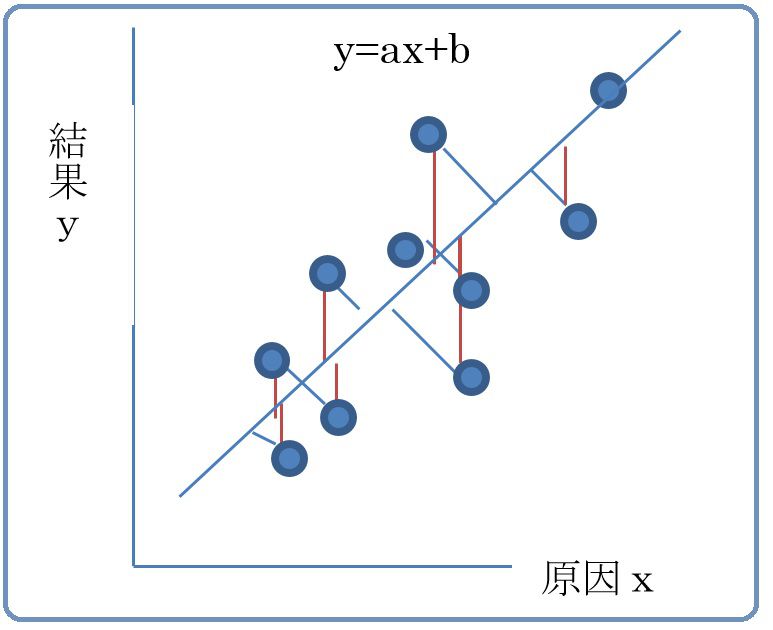
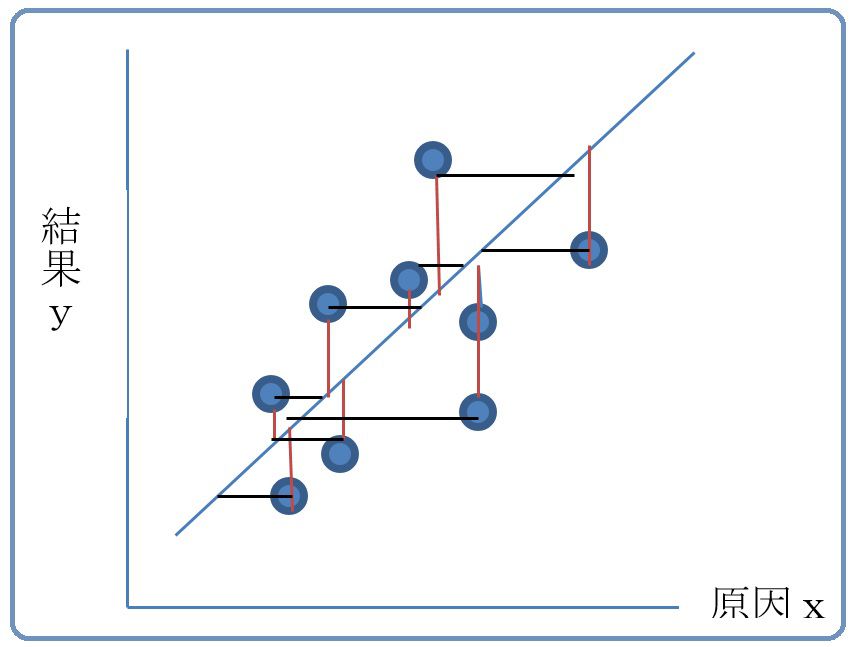
2.回帰と逆回帰の結果は異なる
 ...
...TOP



 ...
...


続きを読むには・・・
重回帰分析といえば説明変数が複数の回帰式をいいます。ものづくりの場面ではもちろん、マーケット調査や心理学など社会科学の分野でも活用されている一方で、単回...
重回帰分析といえば説明変数が複数の回帰式をいいます。ものづくりの場面ではもちろん、マーケット調査や心理学など社会科学の分野でも活用されている一方で、単回...
1.単回帰分析とは 一般的に2変数以上の多変量のデータで、ある1変数を残りの変数で説明しようとする解析法を回帰分析と言います。主となる変数は"目的変数...
1.単回帰分析とは 一般的に2変数以上の多変量のデータで、ある1変数を残りの変数で説明しようとする解析法を回帰分析と言います。主となる変数は"目的変数...
回帰分析の学び直しに厳選記事が無料でお読みいただけます! ◆こんな方におすすめ!=回帰分析を学び直したい!= 「回...
回帰分析の学び直しに厳選記事が無料でお読みいただけます! ◆こんな方におすすめ!=回帰分析を学び直したい!= 「回...
今回は、統計手法の一つである「回帰分析」の解析事例を解説します。 事例として、ほぼ同じタイミングで製造を開始した製品(約200個)に現時...
今回は、統計手法の一つである「回帰分析」の解析事例を解説します。 事例として、ほぼ同じタイミングで製造を開始した製品(約200個)に現時...
製造メーカーG社は製品品質の保証を最終分析結果にて行っていましたが、分析結果を待っての出荷となる為、 生産計画が組みにくい問題点を抱えていました。最終検...
製造メーカーG社は製品品質の保証を最終分析結果にて行っていましたが、分析結果を待っての出荷となる為、 生産計画が組みにくい問題点を抱えていました。最終検...
© ものづくりドットコム / ㈱産業革新研究所
ものづくりドットコムのIDでログイン

まだ未登録の方は、「無料」会員登録で多くの特典が!
Aperza IDでログイン
Aperza IDでのログイン機能は終了いたしました。
今後はものづくりドットコム会員ご登録の上、ログインをお願いいたします





