1．単回帰分析とは

　一般的に2変数以上の多変量のデータで、ある1変数を残りの変数で説明しようとする解析法を回帰分析と言います。主となる変数は"目的変数"もしくは従属変数と呼び、目的変数を説明する変数を"説明変数"もしくは独立変数と言います。相関分析では2変数の関係を対等とみなしているところが、大きな違いです。目的変数に対して説明変数が一つであるものが単回帰分析であり、説明変数が二つ以上のものを重回帰分析と呼びます。単回帰も重回帰も考え方は同じです。

　目的変数をY、説明変数をXとした場合、YとXの関係を説明する式を単回帰式と呼び、単回帰式はY=aX+bで与えられます。aは回帰式の傾きを示し、回帰係数と呼称します。bは切片です。

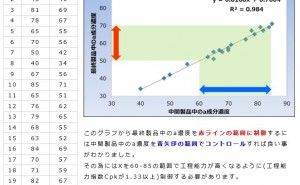
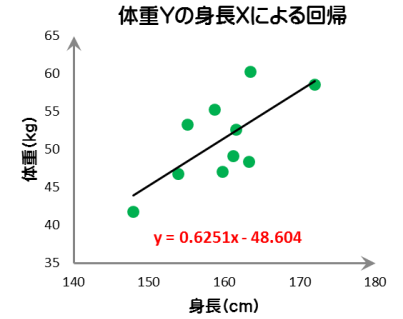　単回帰式はエクセルを用いてXY散布図を描くと、簡単に求められます。右の図1で示すように、マーカー上を右クリックすれば近似式の追加コマンドが出ますから、線形近似を選択すれば図中に表示出来ます。

　この近似式はデータ群の中央付近を通過しているように見えます。この単回帰式は最小二乗法という方法で求めることが出来、その式自体は上述の様にエクセルを用いて簡単に求めることが出来ますが、回帰分析の考え方を理解するため最小二乗法による求め方を次に解説します。　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　図1．散布図と回帰式

2．単回帰のイメージ

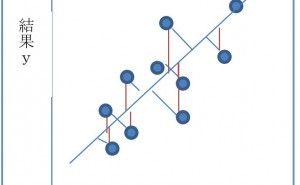
　回帰直線ではあるx_iにおけるYの値を予測する事になりますが、実際の測定値y_iは一定の範囲でばらつきます。つまり一つのx_iに対しy_iが正規分布します。例えば身長と体重の散布データの場合、身長は160cmでも体重は様々に異なる人がいますから同一の値にならずに一定の範囲にばらつき、回帰直線と散布データの関係は下図2のようなイメージとなります。

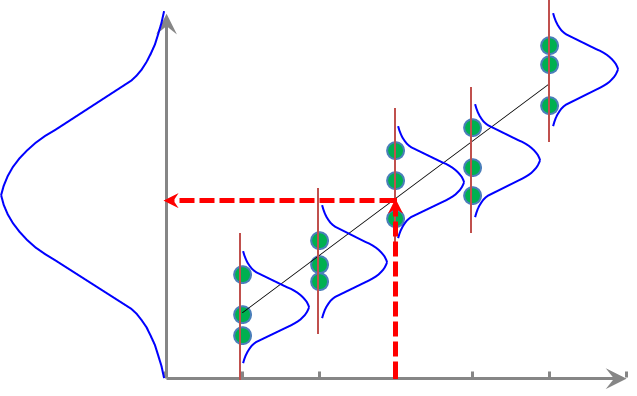
図2．単回帰とデータのばらつき

　Y値をXで上手く説明出来ている回帰式、即ち回帰方程式の精度が高い場合は、直線が各分布の平均点を通過している事になります。上図2で表示している分布の幅が狭ければ、データの多くは直線付近に存在しており、目的変数Yは説明変数X一つで良く説明が出来る事を意味します。
　　

3．回帰式の求め方

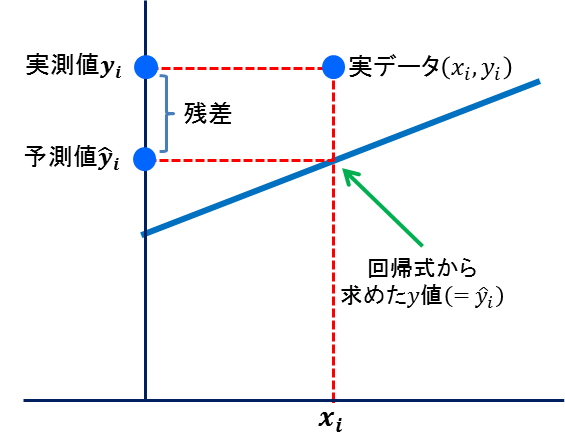
　上の図2からもわかるように、X=x_iの時に回帰式から予測されたY値と観測Y値の間には誤差が生じます。この誤差が最小となる様に回帰係数と切片を求める事になります。

　観測値と予測値の差を下図3のように残差と呼びます。また残差をデータ全体で算出し誤差を定義したものが次式Q_eで表される残差平方和です。



このQ_eが最小値となるように回帰係数と切片を決める方法が最小二乗法なのです。

　このQ_eを最小とするaとbを計算で求めるのは非常に面倒なので、エクセルのソルバー機能を用いて求めることができます。然しながら実際の算出には次に述べる回帰方程式を用いる方法が最も簡便且つ一般的方法です。

　　　　　　　　　　　　　　　　　　　　　　　　　　図3．回帰式と残差の関係　　　　

4．回帰方程式の係数計算

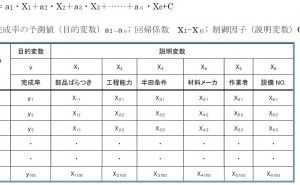
　目的変数Y、説明変数Xの2変数の回帰式がY=aX+bで表される時、回帰係数aと切片bは以下の回帰方程式で求めることが出来ます。

　ここでxとyは変数xとyの平均値で、s_x²はxの分散値、s_xyはxとyの共分散です。

　　　　　　　　　　　　　　　　　　　　　　　　　表1．回帰係数計算用のデータ
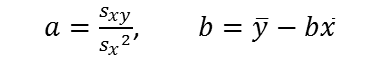
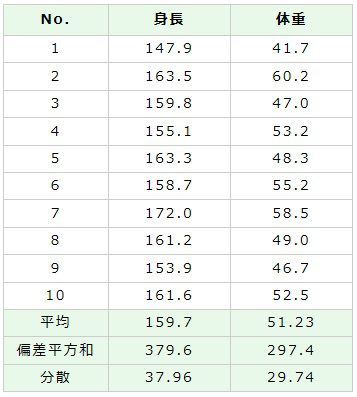　この回帰方程式を使って、右表1のデータで回帰係数aと切片bを求めてみます。このデータは相関分析の相関係数計算で用いているものと同じです。

　まず表1のデータからxとyの共分散を計算します。エクセル関数COVARを用いて計算するとs_xy=23.7となります。

　そして、Xの分散はs_x²＝37.96です。

　これを回帰方程式に入力すると、
a=23.73/37.96=0.625
b=51.23-0.625×159.7=-48.60

即ち回帰式は次式の様になります。

Y=0.625X-48.60