ばねは主要な機械要素のひとつで、さまざまな装置や構造物に広く使われています。このばねの性質を示す法則が「フックの法則」です。ばねの性質とフックの法則については、かつては小学校高学年で、現在では中学校で学びますが、ここでもう一度おさらいしてみましょう。
【目次】
フックの法則とはどういうものか
フックの法則とは「ばねの伸びは弾性限度以下では加えた荷重に正比例する」という法則で、弾性の法則とも呼ばれます。フックの法則が成り立つ物質を線形弾性体（またはフック弾性体）と呼びます。
フックの法則は以下の式で表されます。
F = kx
F：荷重［N］
x：ばねの伸び（変形量）［mm］
k：ばね定数［N/mm］
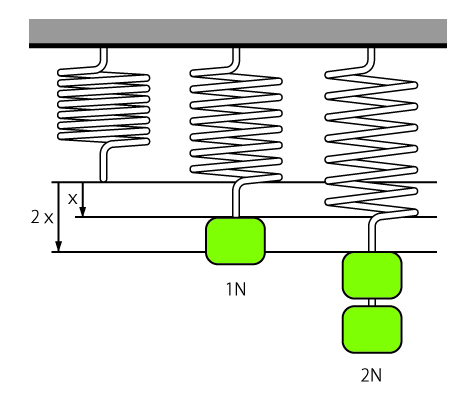【図1】荷重とばねの伸びの関係
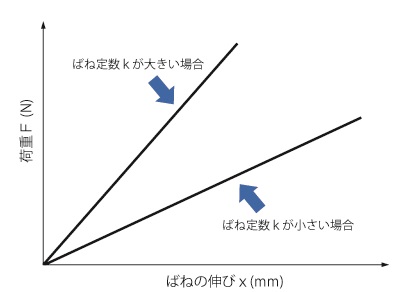
【図2】ばね定数と荷重、ばねの伸びの関係
例えば、1Nの重りを吊るしたときの伸びが20mmのばねに、その2倍の2Nの重りを吊るすと伸びも2倍の40mmになります。このばねのばね定数kは0.05N/mmです。また、1Nの重りを吊るしたときの伸びが10mmのばねに、その2倍の2Nの重りを吊るすと伸びも2倍の20mmになります。このばねのばね定数kは0.1N/mmです。このようにばね定数kが大きいほど、ばねを伸ばすには大きな力が必要になります。
フックの法則は、ばねだけでなく金属・プラスチックなどの材料においても成り立ちます。ただし金属材料では荷重を加えていって弾性限度を超えると、力と変形量が比例しなくなります。つまり、フックの法則が成立するのは弾性限度までということになります。
このように弾性限度内で材料に荷重を加えていく場合には、以下の式が成り立ちます。
σ＝Eε
σ：応力［N/mm2］
ε：ひずみ（単位なし）
E：ヤング率（または縦弾性係数...
