1．統計的推定とは

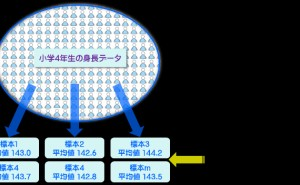
　統計的処理の基本に検定と推定があり、検定とは一定の確率の元で行う◯×判定、言わば定性評価で、推定とは◯×の程度を推定する定量評価です。例えば抜き取り調査において、母集団からサンプルを抜き出し母集団の情報を得るわけですが、抜き出す標本によって推定する母集団の特徴も多少変わってきます。例えば小学校4年生の平均身長を全員測定せずに100名の標本データから推測したなら、抜き出す100名の標本ごとに微妙に平均や標準偏差が異なるはずです。

　この様に標本毎に統計量がばらつくことを標本誤差と呼びます。標本を用いて母集団を推定する場合に、標本の誤差を考慮して平均値や分散値の範囲を推測するのが統計的推定（Statistical interval estimation）です。推定とは標本の”ばらつき”から母集団の姿を推測するということになります。

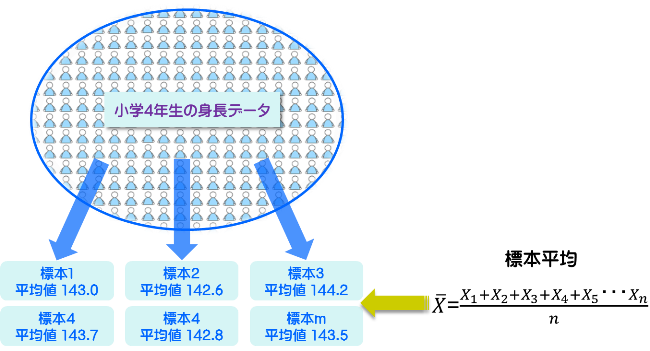
図1　母集団からのサンプル採取
　

2．点推定と区間推定

　実際に母集団の平均値を推定してみます。分布の平均を一つの点で推定するのが点推定です。データの分布が正規分布の場合は、下図2のように標本データの平均値をそのまま点推定値とします。

　一方で区間推定は、標本データから母集団の平均値のばらつき範囲を推測します。この時標本平均の変動する範囲を信頼区間と呼びます。つまり母集団(全データ)の平均値は、この信頼区間の間のどこかに存在すると推定する事になります。推測統計学では一般的に95%若しくは99%の信頼区間を推定します。

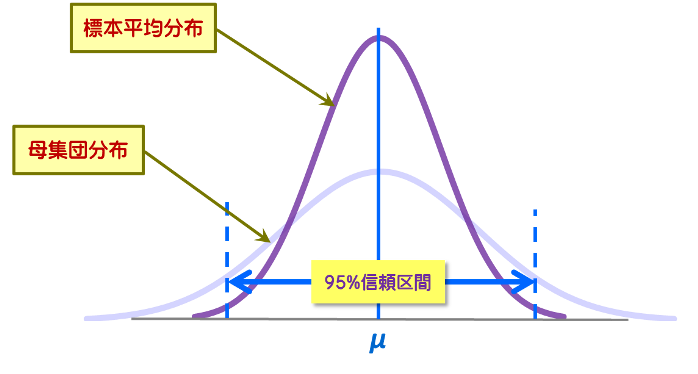
図2　点推定と区間推定

3．95%信頼区間とは

　信頼度95%とは下図3のように、幾つもの標本から計算された信頼区間の95%に母平均μが含まれる事を意味します。例えば5個のサンプルを100セット採取したら、そのうち95セットは、標本から計算した信頼区間の中に母平均が含まれることになります。

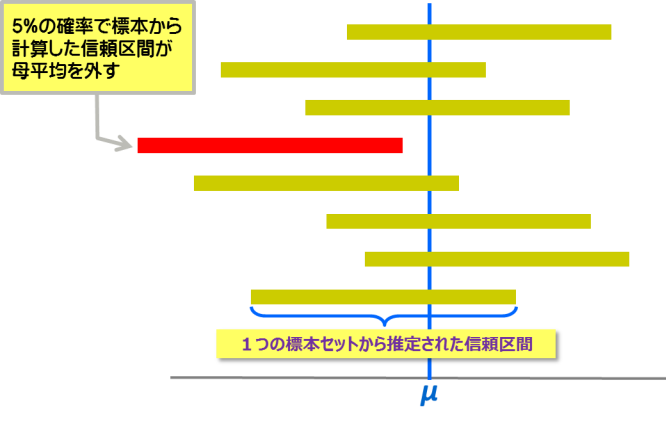
図3　統計的区間推定の信頼度95%

　一般的に検定や推定の信頼度は95%(有意水準5%)を基準としますが、厳密さが然程必要無い場合は90%、逆により厳格に判断したい場合は99%を用いることもあります。信頼度値が高くなるにつれて信頼区間は広くなります。
　

4．母分散が既知の場合の母平均の95%信頼区間の計算

　検定や推定が複雑で難しいと感じるのは、検定や推定の対象によって場合分けが多いからです。例えばある小学生4年生の身長は、5年前に全数検査し平均値と分散値が算出されています。5年前と今回の分布ばらつき(分散)が同じと仮定した場合、平均値がどの様な範囲にあるかを信頼度95%で区間推定する場合の分布は正規分布を用います。下図4は最も基本である母分散既知の場合の母平均の区間推定です。

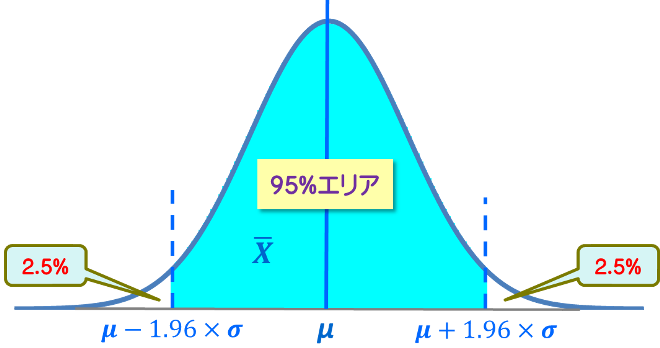
図4　母分散既知の場合の95%推定区間

　95%の信頼区間は青の区間であり、母集団から採取した標本平均もほぼこの範囲にあると考えます。よって標本平均Xは次の式で表される範囲にあります。

 この式をμに対して展開すると、標本平均Xから母平均の推定区間が導かれます。

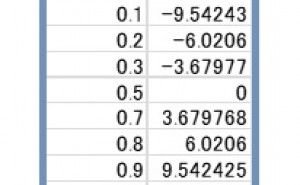
　即ちこれが母分散が既知のケースの母平均推定区間です。母集団から無作為にデータをサンプリングしたら、上式にて計算する事により95%の信頼区間を算出します。 信頼度を係数として一般化したものが下図5となります。式中の1.96は信頼度定数であり、95%の場合は1.96で、90%では1.65、99%は2.58となります。

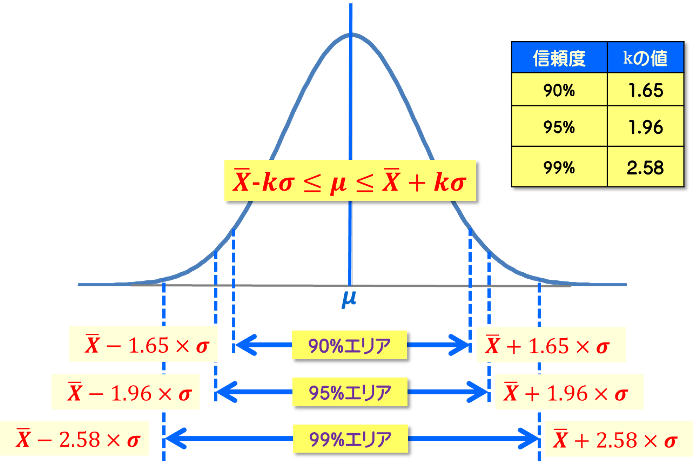
図5　標準正規分布の両側推定区間(90%,95%,99%)

 この定数kはエクセル関数を用いて簡単に計算することが可能です。標準正規分布で計算を行うので関数に入力する平均値はゼロ、標準偏差は1となります。また両側区間推定の場合、95%の確率部分には0.95では無く0.975を入力します。

　エクセルの関数nomrsinv()でも同様の結果を得ることができます。ただしエクセル2007前後で統計関数の書式が変わっていますので使用する場合は注意して下さい。　

5．その他の区間推定法

　上の例では身長の分散が5年前から変化していない前提で区間の推定を行いました。しかし実際には分散も変化している可能性があります。そのように母分散未知として区間推定を行う場合は、正規分布ではなくt分布を用いて区間推定を行います。

　区間推定用いる分布は、検定と同様に推定の対象によって異なり、母平均の推定は殆どの場合正規分布とt分布を用います。分散値の区間推定ではカイ二乗分布を、分散比の区間推定ではF分布を使います。