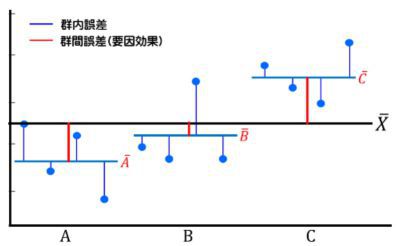
群内誤差と群間誤差 (その2)
投稿日 2015-11-11


続きを読むには・・・
TOP



続きを読むには・・・

眞名子 和義
ムダ・ムラ・ムリの「3ムの撤廃が企業収益向上に繋がる」を信条とし、お客様の"視座"に立ったご提案を致します
ムダ・ムラ・ムリの「3ムの撤廃が企業収益向上に繋がる」を信条とし、お客様の"視座"に立ったご提案を致します

現在記事
1.検定と推定 統計学はデータを数量化して母集団の特徴や傾向を分析したり、母集団からサンプルを抜き取り、この中から母集団の特徴を推測する科学的な学...
1.検定と推定 統計学はデータを数量化して母集団の特徴や傾向を分析したり、母集団からサンプルを抜き取り、この中から母集団の特徴を推測する科学的な学...
統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤...
統計学を学ぶ利点の一つは「誤差」に惑わされなくなる点だと思います。同じ条件で行ったとしても同じ結果が出ない事は数多くあります。所謂ばらつきであり偶発的誤...
今回は、ケンタッキー州にあるマンモス・ケーブ国立公園に行った事からの事例解説です。この国立公...
今回は、ケンタッキー州にあるマンモス・ケーブ国立公園に行った事からの事例解説です。この国立公...
今回は、母集団が正規分布であり、平均値と分散値が既知である場合の検定事例を取り上げます。 小学校4年生のある年の全国身長調査で平均値は143.5cm...
今回は、母集団が正規分布であり、平均値と分散値が既知である場合の検定事例を取り上げます。 小学校4年生のある年の全国身長調査で平均値は143.5cm...

眞名子 和義
改善リンクサービス
ムダ・ムラ・ムリの「3ムの撤廃が企業収益向上に繋がる」を信条とし、お客様の"視座"に立ったご提案を致します
会社概要
-会社概要
© ものづくりドットコム / ㈱ブロードリーフ
ものづくりドットコムのIDでログイン

まだ未登録の方は、「無料」会員登録で多くの特典が!
Aperza IDでログイン
Aperza IDでのログイン機能は終了いたしました。
今後はものづくりドットコム会員ご登録の上、ログインをお願いいたします



