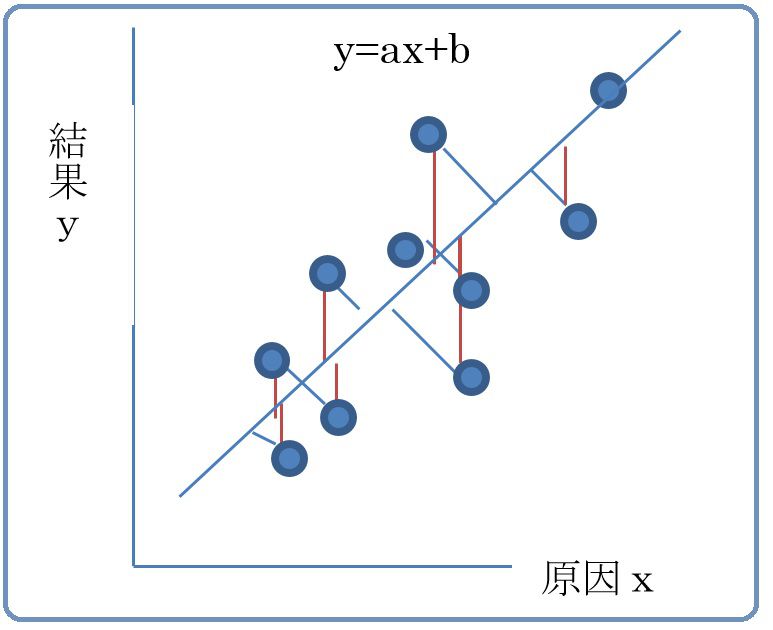
1.回帰直線はyの残差を最小とする
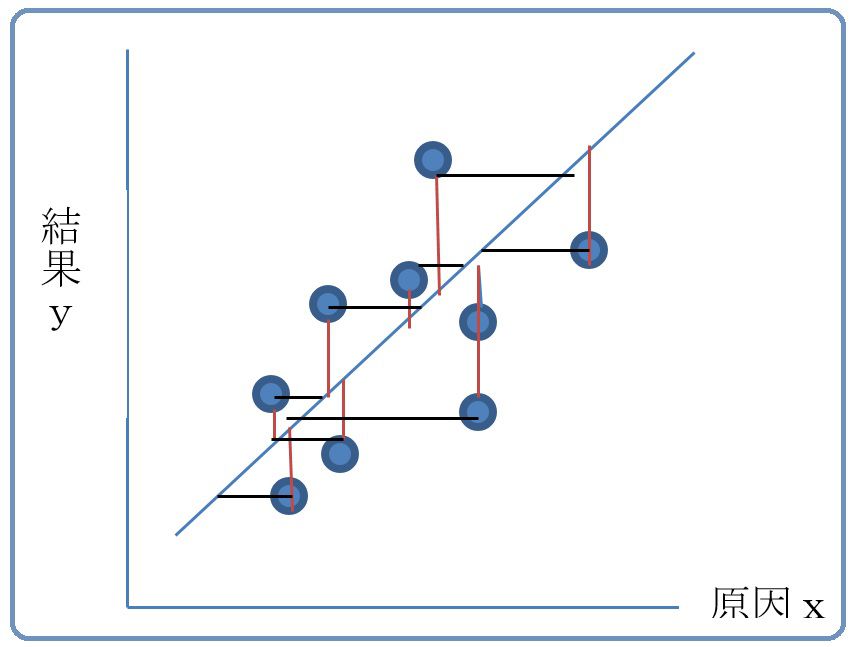
2.回帰と逆回帰の結果は異なる
 ...
...TOP



 ...
...


続きを読むには・・・
ものづくりの場では、様々なデータが存在します。QC7つ道具のひとつである特性要因図(下図)は、特性(結果)に対する要因(原因系)を整理する手法ですが、対...
ものづくりの場では、様々なデータが存在します。QC7つ道具のひとつである特性要因図(下図)は、特性(結果)に対する要因(原因系)を整理する手法ですが、対...
今回は、重回帰分析をおこなうために、ある目的変数に対して相関分析を行い、相関係数の高い項目をピッアップし、回帰式を作成したい場合を...
今回は、重回帰分析をおこなうために、ある目的変数に対して相関分析を行い、相関係数の高い項目をピッアップし、回帰式を作成したい場合を...
母体から、20個とか50個をサンプリングしてきてその平均をとった場合、母体の真の平均からずれますが、どの程度ずれているのかがわかれば非常にアクションがと...
母体から、20個とか50個をサンプリングしてきてその平均をとった場合、母体の真の平均からずれますが、どの程度ずれているのかがわかれば非常にアクションがと...
今回は、統計手法の一つである「回帰分析」の解析事例を解説します。 事例として、ほぼ同じタイミングで製造を開始した製品(約200個)に現時...
今回は、統計手法の一つである「回帰分析」の解析事例を解説します。 事例として、ほぼ同じタイミングで製造を開始した製品(約200個)に現時...
製造メーカーG社は製品品質の保証を最終分析結果にて行っていましたが、分析結果を待っての出荷となる為、 生産計画が組みにくい問題点を抱えていました。最終検...
製造メーカーG社は製品品質の保証を最終分析結果にて行っていましたが、分析結果を待っての出荷となる為、 生産計画が組みにくい問題点を抱えていました。最終検...
会社概要
-会社概要
© ものづくりドットコム / ㈱ブロードリーフ
ものづくりドットコムのIDでログイン

まだ未登録の方は、「無料」会員登録で多くの特典が!
Aperza IDでログイン
Aperza IDでのログイン機能は終了いたしました。
今後はものづくりドットコム会員ご登録の上、ログインをお願いいたします





