技術者や研究者に最も必要とされているスキルは、処理効果を統計的に検証する統計学、そして効率的な実験を計画する能力です。インターネットの発達、グローバル化が進む中、激しい競争に打ち勝つためには膨大なデータを検証する統計学の知識が必須です。しかし、残念ながら日本では統計学の教育が充実しているとは言えず、多くの技術者・研究者が「統計学への苦手意識」を持っています。結果として、実験計画や統計的分析が十分にできていません。
実験計画法は、工学や心理学やマーケティングリサーチや実験関係全般など、さまざまなデータを活用するうえで重要な考え方です。もう少し具体的に言うと、変数間の因果を検討する方法です。今回は、実験計画法とは何なのかを事例をまじえて解説します
1. 実験計画法（DoE）とは
実験計画法とは、開発、設計、生産、製造などで実験する際に、評価する特性と、それに対して影響すると考えられる要因との関係性を調べる方法の体系です。現代統計学の父と言われているロナルド・エイルマー・フィッシャー博士が考案しました。実験計画法は、効率の良い実験方法を設計（デザイン）して、結果を適切に分析する統計学の応用分野の学問のことを言い、実験に際しては、勘、経験だけに頼らず、統計手法を使いながら、より少ない費用と時間で有効な結果が得られるように、計画、実行することが肝要です。
実験計画法は、医学・工学・心理学・農業からマーケティングに至るまで、幅広い業界で利用されています。実験計画には、1因子の水準の変化と影響を把握するための一元配置実験、2因子の水準の変化と影響を把握する二元配置実験、因子が3つ以上の場合の多元配置実験があります。その他にも実験計画法には、分散分析、直交配列表（直交表）直交表を利用して実験数を減らす一部実施法などもあります。
2.「実験計画法」の目的とは
実験計画法の目的とは、「効率的で客観的な結論を得られるように実験を計画すること」です。特に、品質管理のお仕事をされている方からすれば、「実験数を減らすために利用するもの」なのかと考えてしまいがちですが、実験計画法の本質は、「問題を解決するために、データをどういった方法で集めるのか、計画を立てる方法」です。そのため、単純に実験数を減らすという目的ではありません。
通常であれば、実験を行っていく場合には、「要因」などを複数の種類で設定して、それらを一つ一つ組み合わせて実験を進めていきます。そのやり方が基本的に正しいのですが、手間ばかりが掛かってきてしまいます。効率的に実験・試験を行い、進めるために実験計画法があり、複数要因を一緒に実験・試験をしていける方法として、分散分析があります。
分散分析とは、比較したいグループが3つ以上存在する場合に使うことのできる統計手法のことで、3つのグループ間の中でデータにどのような差が出てくるのかを検定します。
3.「実験計画法」のメリット・利点
実験計画法の最大のメリットは、結果として「試験回数を減らすこと」ができる点です。また、データの分析結果としては、条件の内容がどの程度関りがあるのかを数値データで結果が分かるという点も挙げられます。
（１）開発サイクルの短縮ができる点
実験計画は、新機能や他社を圧倒する新技術開発を目指す時に、そうした技術が市場投入後に品質問題が起きないように合理的に検討出来ます。企業は、イノベーションを目指し新しい顧客価値を生み出す独自開発に積極的に取り組むことができるようになるでしょう。
実験計画は、従来の技術が類似製品の開発にも応用できるので、開発にかかる工数を削減できます。そして、開発段階での品質問題が大幅に改善され信頼性の向上につながります。
4.「実験計画法」のデメリット・問題点
実験計画法のデメリットとして、水準を等間隔に設定して実験を行わないと以下の3つのデメリットが発生します。
デメリット1：効率の悪化
3水準を行う実験では、1水準と2水準を殆ど等しい値に設定してしまうと、得られる結果が2水準の実験と殆ど変わらないという悲惨な状況になってしまう可能性もあります。
デメリット2：計算の煩雑化
多水準（複数）の因子で、直交多項式による分解を使って１次効果や２次効果を求める実験の際に、計算がとても煩雑になってしまうケースもあります。この時に使用する係数は、等間隔の場合...
デメリット3：判断ミスの原因になる
不当間隔であることを忘れてしまい、等間隔の要因図式を書いてしまったり、等間隔の公式を使用して分析を行ってしまうなどのミスをしてしまうこともあります。
5. 実験計画法の方法・手法
（１）実験計画法（DOE）の流れ
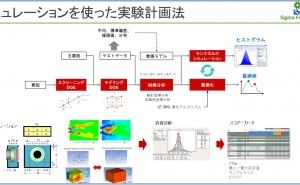
実験計画法では、出力パラメータの変化を効果的（少ない労力で最大限の成果）に捉えることができるように、入力パラメータの値を計画的に変えて実験を繰り返し、データを取得します。次に実験によって得たデータセット（つまり計画的に変更し、かつ組み合わされた入力パラメータの値とそこから得た出力パラメータの値）を使って回帰分析を行い、数値モデルを作ります。最後にその数値モデルを使って、出力パラメータ値が目的値になるように入力パラメータ値を最適化します。実際の実験計画法には技術的にもっと細かいことがあるのですが、以上がおおよその流れです。
実験計画法のフローチャートは、前準備・要因水準決定・わりつけ・実験・データ解析の各ステージで、詳細は、次のマニュアルになります。
6. 実験計画法、実験の効率を上げるために行う直交表の実験
実験計画法での、実験の効率を上げるための直交表の実験について、次のような質問を想定して解説します。
（１）直交表の実験についての想定
ある特性のバラつき要因を探したいのですが、実験の効率を上げるため直交表の使用を考えています。交互作用が不明な10個の2水準因子に対して、すべての交互作用を探しながら実験がしたいのです。直交表を使用するにはどのサイズ(もしくは同じサイズの直交表を複数回)使用すればいいでしょうか。
（２）実験の効率
想定では、すべての交互作用を考慮して実験するということは、すべての組み合わせを見ること（多元配置、つまり総当たり）になります。2水準因子が10個の場合、2^10＝1024通りです。これでは目的とする「実験の効率を上げるため」が実現できません。
実験計画法では、「実験の効率を上げるため」に直交表の実験を行うわけですが、実験効率を上げるためには、固有技術的に交互作用があると（あるいは無いと）考えられる要因を想定することで、直交表の空き列（交互作用が無いと想定した要因に対応する列）に、別の主効果（単一要因）を割り付けることで、総当たりよりも小さな組み合わせで実験を可能とするのです。
したがって、直交表の空き列を作るためには、事前の固有技術的な検討が必要になるわけです。すべての交互作用を割り付けると、総当たりと同じになります。L27直交表にすべての主効果と交互作用を割り付けると、27通りの実験になり、これは3水準因子3個の総当たり（3×3×3＝27）と同じになるのです。
「交互作用の有無を事前に考えましょう」で終わってしまっては身も蓋もないので、次の2つほどアドバイスしましょう。
◆ あくまでも各因子の主効果と因子間交互作用の原因を調べたい場合。
すべての交互作用を調べるのはあきらめて、「すべての2因子間交互作用」を調べることで妥協する方法です。そのこころは、3因子間の交互作用は小さいことが多く、仮にあったとしても技術的に解釈がしづらく、対策に結びつきにくいからです。そこで10因子のコンビネーション（すべての2因子の組み合わせ、つまり45通り）の2元配置（2水準×2水準）の実験を行えば、すべての主効果と2因子間交互作用が分かることになります。実験数は45×2×2＝180通りです。これでも多いですね！※応答曲面法を使用した複合計画では、もう少し小さくなりますが省略します。
もし、独立性が高いと考えられる主効果がいくつか事前に分かっている場合は、直交表の3因子間以上の交互作用列にその主効果を割り付けるというのが現実的です。L16なら、15列のうち4列が主効果、6列が2因子間交互作用の列ですので、残りの5列が3因子間以上の交互作用列です。ここに独立性の高い因子を割り付ければ、もとの主効果4因子と合わせて、同時に9因子が検討可能になります。ご質問では10因子ですので、L32が必要ということになります。これなら現実的な実験の大きさです。
◆ ばらつきの原因を調べるのをやめるという発想。
原因候補の10因子をL12直交表に割り付けて、いずれの12条件でも特性値yがばらつきにくいように、yの設計そのものを変更（改善）する考え方です。これが品質工学における機能性評価、パラメータ設計の考えかたです。この技術については、このサイトにもたくさんの情報がありますので、参考にしてください。
7. 事例：実験計画の水準ずらし法とは
今回は、ポリマーを合成し、あるノイズに強くしたい事例で、品質工学を使う場面を想定します。合成に用いる因子間の交互作用が強く、通常の直交表では合成できない実験が多数できてしまう事例で、水準ずらし法での解決ですが、次のように問題点を2つに分けて解説します。
（１）合成できない組み合わせができてしまう問題。
この場合、合成できる範囲があらかじめだいたい想定できているのであれば、それを制約条件とするような関係式を作って水準を決めます。反応温度と反応時間なら、反応温度が低いときは長めの時間の3水準、温度が高いときは短めの時間の3水準という具合です。固有技術的な知見もいると思います。
直交表の条件中（例えば16条件中）、いくつか合成できない条件があっても、欠測値の処理を行えば推定できる場合も多いので、「当たりを探す」とい意味ではあまり制御因子の水準を狭めすぎないほうがよいと思います。
また、範囲に制約があるということは、自由度（数学的な意味です）が１つ減るわけですから、独立変数の数に気を付けてください。たとえばAとBの組成比が合計0.5と決まっているような場合は、Aを決めればBは従属的に決まるわけですから、Bを独立な因子として扱うことはできません。
（２）制御因子間に交互作用があって、正しく推定できない問題。
水準ずらしを行うケースとして多いのはことらの場合です。目的は制御因子間の交互作用の消去です。化学合成などの分野ではこの問題のほうが圧倒的に大きいはずです。どのような水準ずらしをすれば交互作用が消えるかは、固有技術（工学）的な問題です。AとBの値をそのまま水準にすると交互作用がでるが、Aの水準を決めた上で、Bの水準はAの値との比率で決める（たとえば、B1＝0.5A、B2=1.0A、B3＝1.5A）などのやり方です。
また化学系の場合、制御因子の選ぶ際に温度や時間や組成といった、実験者が直接操作できる因子を選びがちですが、それが適切なのかどうかもよく考える必要があります。化学系の実験計画法では、品質工学は交互作用や多特性になる問題があって、かなりノウハウがいります。専門家のご指導を受けられるのがよいと思います。コンピュータシミュレーションができず、実験も大規模になることが多いので、できるだけ手戻りがないように事前に手を打っておくべきです。
8. 実験計画法の活用例
（１）シミュレーションを使った実験計画法
実験計画は、現物ではなく、今ではシミュレーションを使って行っています。機械設計、電気回路設計、熱設計など、今は設計のほとんどのがコンピュータを使って行われています。また設計したものをコンピュータ上でシミュレーションすることが普通です。シミュレーションの精度も高く、実務では全く問題のないレベルに達しています。事例を、いつか紹介します。
【コントロール室の各装置の配置を実験計画法で最適化】
コントロール室には熱源である様々な装置が配置され、コントロール室の温度を上昇させていた。温度上昇を最低限に抑えるために、各装置の配置をシミュレーションと実験計画法によって最適化した。
【冷却ファンの筐体とファンの位置を実験計画法を使って最適化】
冷却ファンからの気流を最大限にするために、ファンを格納する筐体のサイズ（高さ、幅、奥行き）と筐体内でのファンの位置を、シミュレーションと実験計画法を使って最適化した。
【基板埋め込み型のトランスの大きさを実験計画法を使って最適化】
基板埋め込み型トランスのパターン幅やピッチ、厚さをシミュレーションと実験計画法を使って最適化し、狙ったトランス特性が得られるようにした。
9. 実験計画法について学ぶなら
実験計画法について学ぶなら、セミナーもおすすめです。
ものづくりドットコムでは毎月約1,500以上のセミナーを掲載しています。
10. まとめ
（１）実験計画法、実務・運用上の課題
実験計画法は素晴らしいのですが、次のような実務・運用上の課題題に直面します。
パラメータの値を計画通りに変えられない
すべての実験計画を行うと莫大な時間がかかる（現実的ではない）
計画通りにパラメータの値を変えると莫大なコストがかかる（現実的ではない）
実験のために通常業務（設備）を止めることができない
実験のために特別な設備を用意できない
（２）最適化結果検証
シミュレーション結果は十分正しいということを、シミュレーションを使った実験計画法は前提にしています。すなわちシミュレーション結果が正しくなければ、この実験計画法は成り立ちません。そこで現物を使って、実験計画法で得た数値モデルとシミュレーションから得た数値モデルは十分に近いということを証明するようにしています。
◆【特集】 連載記事紹介：連載記事のタイトルをまとめてご紹介！！