
1.オンライン品質管理の問題を解決
オンライン品質工学(OLQE)は消費者の品質について生産コストと生産段階の品質のバランスを扱います。製造工程中の作業者の仕事は、チェック(工程管理)ですので、(フィードバック)制御によって機械とか工程を管理します。品質工学は品質の損失関数を用いることで、(オンラインの品質管理の)問題を解決します。[1]
2.オンライン品質工学の考え方
タグチメソッドでは「オンライン品質工学」として、品質特性が許容限界を飛び越えないようにするため、調整限界を設定してこれを越えた場合に、目標値になるよう「工程パラメータ」を調整するものです。これを「オンラインフィードバック制御」といいます。シューハートの管理図と異なり、管理限界としての3σを基準としません。損失関数に従い、機能限界と規格限界を設定して、基準外になった場合には原因を追究しないで、パラメータを調整することで目標値になるようにコントロールするものです。
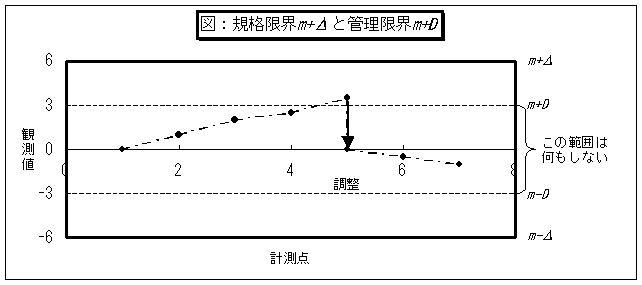
オンラインフィードバック制御の最適化手順は、以下のように行います。[1]
まずパラメータを整理します。
品質特性の規格値:m±Δ0 この規格を外れた場合には不良品となります。
不良品(規格外れ)の損失:A円 規格外れとなった製品の原価と廃棄の費用を見積もります。
計測コスト:B円 工程検査を行うためのコスト(人件費)を見積もります。
調節コスト:C円 調整限界を外れた場合にパラメータを調整するためのコスト(人件費)を見積もります。
以上を用いて定式化します。
計測間隔:n0個 工程で何個毎に検査しているかを求めます。
平均調整間隔:u0個 実績データから平均何個毎に調整しているかを求める。概算でもよいです。
調節限界:D0 現状ではこの調整限界を外れた場合に調整を行います。
これらのパラメータを用いて、製品1個当たりの総コストを求めていきます。
生産工程では一般的にn0個間隔で、B円のコストで計測しているから、1個当たりの計測コストは以下のようになります。
計測コスト=B/n0(円) 1式
同様に平均u0個単位で調節を行っている訳だから、調節のコストは次式で求めることができます。
調節コスト=C/u0 (円) 2式
任意の調整限界D0に対して平均調整間隔がどうなるかは、個々の工程ごとに変化し、それは工程の安定性に関係してきます。工程の変化は、さまざまな外乱の影響、工具などの磨耗、計測誤差などの影響を含んで複雑です。ここでは、平均調整間隔u0は、調整限界D0の2乗に比例すると考えます。最適調整限界Dを決めた後、その仮定のもとに、平均調整間隔uを予測し、実際の観測結果と比較してその仮定の正しさをチェックできるので、その仮定は第一近似と考えていることになります。ここで、
実際の調整間隔(見積):D0個
そのもとでの平均調整間隔uoを調査して比例定数λを次式で求めます。
![]() 3式
3式
λをuとDで記述して、次式を得ることができます。
u/D2 =uo/(Do2 ) 4式
したがって、最適調整限界Dを決めたあと平均調整間隔uを次式で予測します。
![]() 5式
5式
この仮定のもとで計測調整コストは1式と3式を加えて
![]() 6式
6式
となります。ここでCは調整限界を飛び出た際に行う「調整作業」のコストです。
次に、このような計測調整を行ったときの品質水準はどうなるのでしょうか。計測誤差を考えなければその損失は次式で与えられるものとなります。その理由は品質工学では規格内であっても目標値からの差があれば損失が生じるとされ、目標からの差の二乗で計算できると考えます。これを損失関数といい、次式で計算します。
L(y)=A/∆2 (y-m)2 7式
で与えられ、1個あたりの品質による損失は(y-m)2の期待値を求めればよいのです。
ここに調整限界をm±Dとしたのだから、前項の図からも分かるように、特性値はその範囲内でほぼ一様分布*すると考えられます。その時の平均二乗誤差(分散と同義)は、D2/3で与えられます。
*ここでは、一般的な正規分布とするのではなく、ランダムな変動を考えているので、一様分布が妥当と考えています。作業によりドリルの刃先が摩耗するとか、制御系に油圧を用いているため、時間とともに温度が上昇するなど。
したがってその平均二乗誤差(分散)は
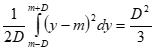 8式
8式
で与えられます。
また、計測間隔nでチェックしているとき、前の計測点では「調整限界内」、今回の計測点では「調整限界外」の時、調整限界外になった生産個数の平均はほぼ(n+1)/2個で、またタイムラグlもその仲間です...



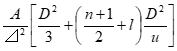 10式
10式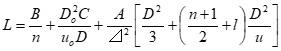 11式
11式 























