他の技法解説で、母比率の推定について視聴率を例に取り上げました。その中で『 標本誤差 』について述べましたが、これ以外にも『 非標本誤差 』があります。1．『 標本誤差 』
例えば国民全ての年齢を調査した平均年齢と無作為に選び出した1000人の平均年齢はピタリと一致せず多少の誤差があると思います。 視聴率も同様で、関東エリアであれば地域全世帯の全数調査で出た結果と、500戸の抜き取り調査結果が完全に一致する事は無く、相応の誤差が生じます。
この真の値と標本調査の結果の差異を標本誤差と言います。 つまりサンプルにより生じる誤差です。標本誤差は誤差の範囲を計算により求めることが出来ます。それが統計的区間推定です。標本から求めた視聴率であれば、その値を基準としてエリア全世帯の視聴率が含まれるだろう区間を統計的に求める(推定する)わけです。標本誤差を小さくするには標本数を大きくします。標本数を大きくしていけば最終的に母集団と同じになりますから誤差は無くなります。
2．『 非標本誤差 』
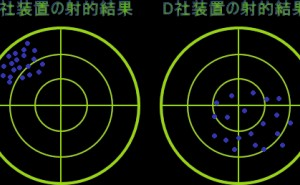
非標本誤差ですから採取したサンプルから生じる誤差とは異なります。例えば、サンプリングでのデータの偏りを防止するには無作為に行う必要があります。 恣意的に行えば標本誤差とは別の誤差が生まれます。これも”非標本誤差”に含まれます。
平均年齢で言えば最も平均年齢が高い県と、低い県の差(レンジ)は8歳もあります。もし同一県から全てのサンプルを採取したら全国平均との誤差は大きくなるでしょう。非標本誤差は他にアンケート調査の未回答や誤回答、集計ミスなどがあります。
アンケート調査では『有効回答数』の様に非標本誤差を小さくするよう予め無効なものを排除して集計してある場合もあります。
その他非標本誤差はミスやアクシデントにより生じものが多く見られます。計算により求めることは出来ませんので出来るだけ生...
