1.ばらつき
同じ条件で採取したデータであっても、一定の範囲内で変動しています。 即ちばらつきがあるということです。 ばらつきが大きいとは広い範囲にデータが分布している事であり、ばらつきが小さいとは狭い範囲に分布している事になります。
特性の改善には平均値の改善とばらつきの改善の二つがあります。
たとえばスマートフォンのバッテリー仕様値がP社が平均200時間、S社が平均300時間だったとすると、平均だけならばS社のバッテリーが優れています。 しかしP社のばらつきは180-220時間に収まり、S社は100-350時間だったとしたら如何でしょうか? S社製の方が仕様を満たさない外れ品に当たる可能性が高いですね。
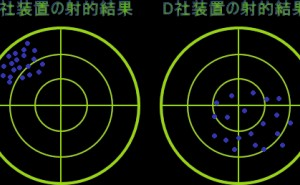
次にC社とD社がそれぞれ投射マシンを開発し、それぞれの投射結果は下の図1のようになったとします。
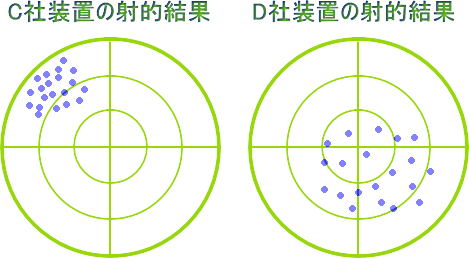
図1 射的装置のばらつきイメージ
両社ともに性能に問題があるのが容易にわかると思いますが、C社とD社の装置を改善するならどちらが容易でしょうか? 一見するとC社は的の中央から大きく外れ、D社は一部が中央付近に当たっているのでD社製の修正が容易に思えます。 しかし実際はばらつきの少ないC社の方が調整は容易です。なぜなら、C社は狙いは大きくずれているもののばらつきが少ないので、方向だけを調整すれば問題ありません。 一方のD社は、方向に加えてばらつきを生み出している要因を見つけ出し、解消する調整を行う必要があるのです。
特性の改善には平均値の改善とばらつきの改善の2種類があるのです。多くの人が最初に平均値の改善に注力しますが、それはばらつきが問題無いレベルであればこそです。 ばらつきが大きいと、平均値を改善しようとしても、良くなっているのかどうかの判断が難しいのです。
射的の例では円を描くようにばらつきが観られますが、実際はいびつなばらつきをする事も珍しくありません。 まさしく平均がどこかを判断するのが難しく、改善の方向性が絞れない事態になりがちです。
2.母集団とサンプル
同じ条件下にある集団の群全体を"母集団"と言います。 例えば全国の30代の男性の体重を調査する場合、30代男性全体が母集団となります。仮に30代男性が1000万人居たとすると、すべての人のデータを取るのはほぼ不可能です。そこで図2のように一部のデータを取り、30代男性の体重分布を推測します。
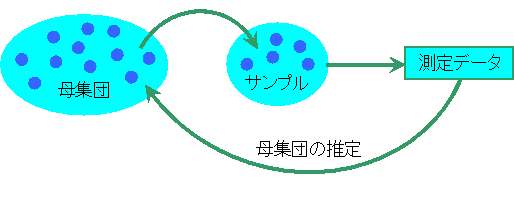
図2 母集団と標本イメージ
この一部の人の体重データが「サンプル(=標本)」であり、統計的にそのデータから母集団の姿を推定する事が可能です。 サンプルは母集団推定の手がかりであるため、データ採取には偏りを持たせないように「ランダムに」サンプリングしなければなりません。
公園でジョギングをやっている人を集めてデータを取ったら、30代の体重の代表データとして妥当でしょうか?ランダムサンプリングとは無作為に標本を集める事です。何かしらのバイアスをかけてデータを選んでしまうと、その後の分析がすべて無意味になり、そのデータから精度高く母集団の傾向を探る事は困難となります。
もし母集団がA県のB村で対象が300人程度なら全員の体重を測定する事も可能でしょう。 この場合は対象すべてのデータを用いるのでサンプルによる統計的推定は必要ありません。しかし...