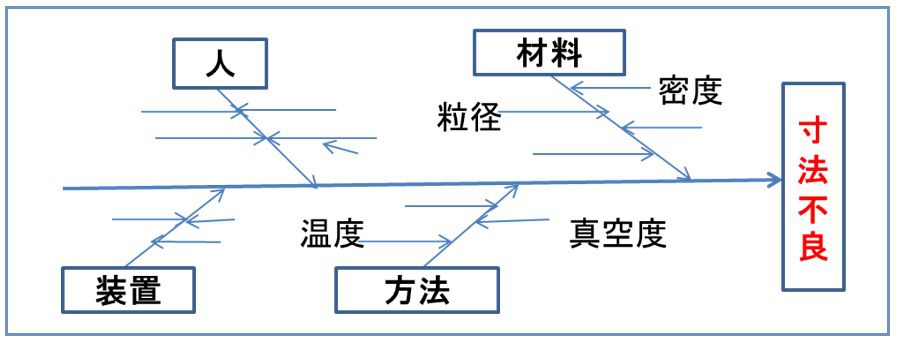
ものづくりの場では、様々なデータが存在します。QC7つ道具のひとつである特性要因図（下図）は、特性（結果）に対する要因（原因系）を整理する手法ですが、対策を決めるにはデータで判断することが必要なことも多いようです。又、コストのかからない方法を採択する必要があります。
例えば、密度、粒径、温度、真空度がピックアップされ、これらの工程内データと寸法不良との関係が知りたい。寸法はこれら複数要因で決まるので、単回帰分析では不十分だ。そこで、下記モデルが考えられるます。
y（寸法）＝ C0＋C1×密度+C2×粒径+C3×温度+C4×真空度 （式1）
この式の係数（C0, C1, C2, C3, C4）を決定すれば、関係が明白となります。密度や粒径がわかれば、寸法出来栄えが予測できるし、逆に温度をいくらにすれば、寸法を規格に入れられるのかも逆算できます。式1では、全て1次線形式であって、粒径や温度には平方根や2乗比例を考えるべきだということもあるでしょうが、現場データのような狭い範囲では、これで十分です。こういった場合、従来、重回帰分析という多変量解析が使われていますが、1次線形式と言え、昔は大変な解析工数を要しました。もちろん、大型計算機のある企業なら別ですが、電卓しか使えない環境下のメーカでは無理でした。重回帰分析は、分散・共分散行列の逆行列を計算するため、手計算ではまず無理なのです。パソコンでも20年前では容易ではありませんでした。一方、パソコンの性能発展、普及は今まで困難だったデータ解析を容易にしました。意外にも、この辺の事情に気が付いていないことが多いようです。重回帰分析はクリック数回でできる時代になりました。
注意しなければいけないのは、要因間に相関係数が高くなった場合です。説明は省きますが、予測精度が悪化します。（多重共線性問題）しかし、対応策は簡単です。コストのかかる要因、管理しにくい要因の方を削除すればよいのです。元々、相関が高いのであれば、どちらかの情報でよいでしょう。又、要因間の単位が違っていると、係数の大きさで効果の大きさを判断できません。cmとgrでは比較の意味がないのです。そこで、各データの標準化（平均をひいて標準偏差で割ると単位が消え、平均がゼロ、標準偏差が1の分布に変わる！）が必要となります。これも簡単にできるので、この値を用いて重回帰分析をすれば、各係数の大小が効果の大きさとなり、管理の軽重に役立ちます。むしろ、今も昔も重要なことは、出てきた結果の読解力です。これには、回帰の寄与率や回帰係数に付随したp値、標準誤差、信頼限界などが出力されます。この解釈からのフィードバックが肝心となります。さらに、よく勘違いされていますが、説明変数（式1の密度や粒径等）がデータ数より多いと、見かけ上の寄与率が高まるので、自由度調整済み決定係数に注目することが大事になります。このことからも、役に立たない説明変数は消し去った方がいいわけですが、この方法を誤ると大きな解析ミスとなります。このへんは、専門家とよく相談しながら進めるほうが手堅いでしょう。
計算コストは、少ないにこしたことはありません。たしかに、よくわかりもしないデータをいれていては、「ごみを入れてもゴミしか出ない」となる主張もあります。しかし、本来有用なデータでも解析できなければ何の役にも立たないので、「まずやってみる」ことも時と...
して必要です。その際、「さっさとできる」ことはいいことです。従来、有用でも困難だった手法を、今一度、ものづくりの場で活用すべきです。現代は、それが簡単にできる時代ではないでしょうか。
この文書は、 2016年5月5日の日刊工業新聞掲載記事を筆者により改変したものです。