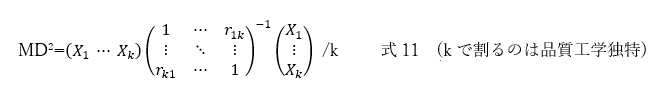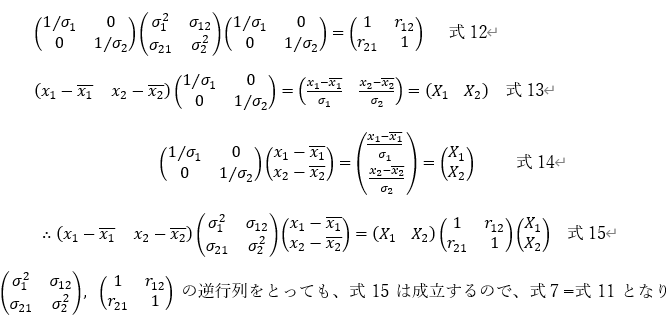今回は、MT法やMTA法で使われるマハラノビス距離の話をおさらいします。余因子の話からは一旦離れますが、次回また扱います。
1.MT法、MTA法での距離とは
まず、MTA法というのは、MT法のアンチテーゼとして生まれたものなので、MT法の数理から入ります。
MT法は、マハラノビス距離を相関行列で説明している本が多いですが、初学者には、却(かえ)って難しい。式の意味からは「普通の」、「分散」、「共分散」のほうが分かりやすいでしょう。
MTとは、マハラノビス・タグチの略なのですが、基準尺度を計算するところに、タグチの出番はなく“マハラノビス”そのものです。ここからスタートしましょう。
マハラノビス距離を一言でいえば、平均からの離れ具合を、ばらつき(標準偏差)で評価するというものです。例えば、平均から遠く離れたものは、距離が長いということですが、その標準偏差が非常に大きければ意味がないでしょう。平均が5mで、そこから15m離れたら、10m離れたことになって、大きいように思われるが、このときのバラツキが12mあるなら、誤差範囲です。でも、バラツキが1mmなら、すごく離れていることになる。ご存じの「偏差値」は一次元のマハラノビス距離の変形版です。
![]()
10倍して、50を足しているのは、試験における満点が100点、最低が0点の場合が多く、偏差値の感触が実際の得点の感触に近いようにしたかっただけ、とのことです。
本質的には平均から離れている点数が、バラツキの何倍かを表現しています。
これを多次元展開してn次元のマハラノビス距離は、以下のように計算します。
表1 データ形式
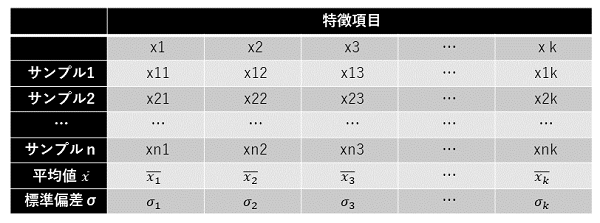
各サンプルごとに、
![]()
この平方根をマハラノビス距離とします。項目数kで割るのは品質工学専用です。この式で、全然問題ないのですが、品質工学では、相関係数から入っている場合が多いのです。意味がよく分かるというのでは、式7ですが(要は、平均からの離れ具合がσの何倍かというもの)、相関係数でも同様の表現ができて、相関行列が簡単に出せる時代にあっては、こちらのほうが実用性も高いので、ここからはこちらで説明します。
と、その前に、標準化の話が必要です。
標準化というのは、あるデータから平均を引き、σで割ったものです。一次元のマハラノビス距離に対応します。これは、非常に重要な変換です。例えば、重回帰分析などで、係数の値が大きくても、変数の単位がcmとm、kgとm、では係数の値が大きいから、効果が大きいとはいえません。こんな時、標準化しておけば、変数の単位が消えて、効果の大小が判断しやすいです。
もうひとつは、標準化すれば、共分散の値が相関係数になることです。分散は1になります。実際に数値計算すれば、分かりますが、2次行列で証明しましょう。

でしたから、今、s11=s22=1として、r12=s12 当然、r21=s=21 式10
よって、式8が成立します。
これは、2元の相関についての話ですが、当然、n次の相関行列についても成立します。標準化されたデータの分散・共分散行列は相関行列に一致するということです。逆に、相関行列をとってしまえば、データを標準化した分散・共分散行列をとっていることになります。マハラノビスの距離は、標準化を通して同じことをやっているわけです。
むしろ、相関行列ならエクセルでも一回で出るので、この方法の方が簡単です。
相関行列を使ってマハラノビス距離を表わすと、以下のようになります。
...