【効率的な実験手順を考える 連載目次】
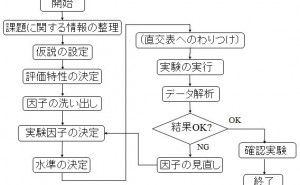
1. 全体の流れ
2. 実験の目的と評価項目、方法、目標を設定する
3. 因子のリストアップと選定
4. 直交表実験の準備と実行
5. 直交表実験の解析と確認
1.実験因子の抽出
実験手順の中で、ある意味ここが一番重要なステップです。目的とする効果に対して有効な制御因子が実験に含まれていないと、どんなにうまく実験、分析しても芳しい結果は得られません。このステップだけは手法の問題ではなく技術者の知識、経験と感性に依るところが大ですが、それでも効果的に拾い上げるために次のような幾つかの手法があります。
(1)特性要因図
QC7つ道具のひとつ「魚の骨」です。単に因子を羅列するのではなく、大分類から順を追って細分化していくことで因子の見逃しを防ぎ、新たな因子を発見しやすくします。
大分類がさっと思い浮かばない時は一般的な4M(Machine, Man, Method, Material)を使ってみましょう。
(2)ブレーンストーミング
自分で思いつかない時は、その事象に対して知識、経験のありそうな人、場合によっては全く違う分野の人も呼んで特性要因図を一緒に作ってみましょう。アイデアが煮詰まったら、みんなで製造、開発現場へ行き、実物を見ながら議論すると発想がまた広がります。競合製品やその情報を議論することも有効です。
(3)特許、文献
特許、文献は技術ネタの宝庫です。特許は特許庁Webサイト、文献は国会図書館Webサイトなどでキーワード検索が可能です。
(4)その他アイデア発想ツール
このサイトの中にたくさん紹介していますので参考にしてください。
因子は充分数え挙げられましたか? 実験目的にもよりますが、10や20要因ではまだ見逃しがあると思われます。50個を目安に挙げてみてください。こんな因子は有意ではないだろうといった先入観念は危険です。当面実験に組み入れなくても、特性要因図に記入しておくことは後々第2次の実験が必要になった時に役立ちます。
2.実験因子の選定
さて50個の因子が出てきたら、次はその中から制御因子を選別します。たとえ目的に対していくら効果が大きくとも、作業者やその日の天気といった要因は生産する際に自由に設定できません。Aさんが作れば良いと分かっても一人ですべてを作るわけにいかず、雨の時に優れた特性が得られるからといって、晴れの日に生産しないわけにはいかないですよね。
しかしAさんとBさんの作ったサンプルに有意差が現れたら、その違いを見つけることで制御因子に転換できる可能性が出てきます。二人の間で工程の順番や処理時間、力の入れ方といった項目が違っているならば、それらを制御因子として実験で評価しましょう。
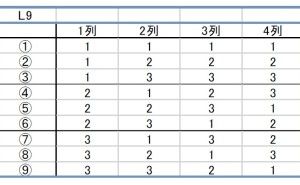
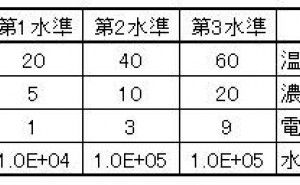
次に制御因子の中から最初の実験で評価するものを選定します。より影響が大きそうな因子から順に選んでいくことになります。直交表を使った実験であればよく使われるものがL8、L9、L12、L16、L18などですから、一回で評価できる因子は4から15となり、選択する直交表も考えながら複数の人で特性要因図から選定していきます。実験を惜しまず5から8因子をL18などで評価することがロバストな設計をするためのコツです。たとえ有意になりそうな因子が3つしかなくても、それらに次いで可能性のある因子をいくつか組み合わせることで、広範な環境で通用する設定を導き出すことができるの...