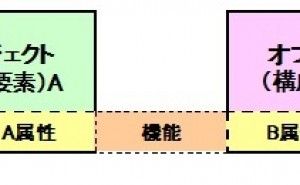
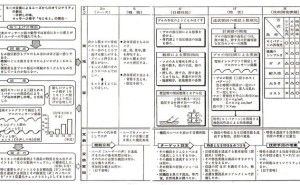
計測の世界では、誤差(精度)を求めることが必要ですが、誤差は真値―計測値で定義されているため、真値が分からなければ誤差は求められません。それにもかかわらず科学技術問題では、質量や長さや時間や電流値などの、物理特性の精度を問題にすることが要求されます。
世の中では真値があるとして誤差を求めていますが、真値は約束事であって実際には存在しないのです。そこで、品質工学では、真値不明で誤差を求めることを考えました。体重計の精度を求める具体的事例で説明してみましょう。
体重計の誤差は「真値-読み値」で表されます。
1.準備するもの:家庭にあるバケツ2個と人間一人
2.実験:水の入ったバケツを2個用意します。ヘルスメータでバケツの水の重さが全く同じで3kg(何キロクラムでもよい)になるように水量を調節します。
次に、使用条件として、硬い床の上(N1)と軟らかいマットの上(N2)で、下表のような実験を行います。人間が乗る位置をノイズにしてもよいでしょう。
| M1(人)kg | M2(人+バケツ1個) | M3(人+バケツ2個) | |
| N1(硬い床の上) | y11(77.0) | y12(79.5) | y13(82.5) |
| N2(軟らかいマットの上) | y21(78.0) | y22(8... |