♦ 日本文化伝承する規矩準縄術
1.曲尺と発音
棟梁(とうりょう)をはじめとする大工さんたちの腕の素晴らしさは、日本の家屋が地震に強いことでもよく知られていますが、彼らは経験則で適当に設計しているのでしょうか?いえいえ、そうではないのです。まず、大工の棟梁の使っている曲尺(かねじゃく)。この道具はすごいのです。指矩(さしがね、指金)とも呼ばれますが、どこかで聞いたことがある?そうです、人に裏から指図しているという意味の「さしがね」の語源ともいわれています。曲げて使ったりもできる変形に富んだ金属製で「かねじゃく」と呼ばれますが、直角に曲がっている尺(物差し)なため、漢字では曲尺という表記になります。法隆寺や大阪城建築等の際、吉凶の寸法を占う尺度(1寸5分単位で1、4、8倍を吉、他は凶)としても使われました。
今の大工さんはもう計算機頼りで「曲尺は精度が悪いから…」と使わないという方もいらっしゃいます。しかし、計算機では現場で通用しないことも多いのです。何せ、相手の木材は真っ直ぐとは限りません。手に持っている道具を直接木材と比べて出来上がりの状態を予測しているのです。曲尺には表目と裏目があります。彼らのすごさは、メートル法になっても、1/33m単位と主張して生き残っていることです(もちろん、一寸単位!一升瓶を1.8リットル瓶というのと同じ)。表目は普通の定規なのですが、裏目は√2とπを単位に作られています。これらを使って、大工さんたちは超絶技法を演じているのです。基本的には直角三角形の定規なのです。
下図をご覧ください。これは屋根の形です。ピタゴラスの定理は我が国では、股勾弦(ここうげん)の定理と呼んできました。和算というと特別な数学者のやっていたことのように思われるかも知れませんが、建築現場の数学として確立されていたのです。もちろん、勾配の語源はこの「勾」なのです。
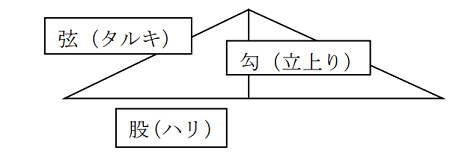
2.平方根もできる ~ 裏目に隠れる数学理論
曲尺を使い、大工さんは上図の屋根の設計をするだけではなく、丸い材木の切り口だけを使い、そこから取れる角材の寸法を簡単に出してしまいます。まず、直径はどうして出すのでしょうか?下の図を見れば分かるように、直角三角形と円の関係で、曲尺の角を丸材の端に当てれば、すぐに直径は求まります(幾何学ではコンパスを使う方法を習いますが、三角定規の使い方はあまり教えない?)。そこで裏目を使うのです。すると、√2の関係で取れる角材の寸法が出せるのです。
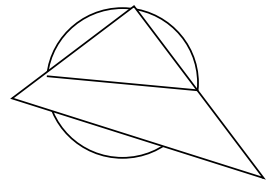
曲尺による一般的な方法として平方根が出せます。それは、下図の様にすると、ピタゴラスの定理からb=√aとなることを使います。
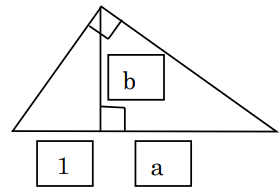
さらに、3次元もできます!大工さんによく注文されるのは、今の枡の2倍の量を測れる枡(ます)を作れ、という命題です。この問題には曲尺を2つ使います。今度は2の立法根を出す問題。2つの曲尺を繋いで出すのですが、どうするのか考えてみてください。曲尺は立方根も簡単に求められる、素晴らしい道具なのです。
3.現場にあふれる大工道具と数学
Nx9(N=1,9)を指で表示する方法を知っていますか?両手を広げて、左からN番目の指を折り、残りの立っている指の左側が十の桁、右側が1の桁です。例えば、3x9なら、...