♦ 限りある時間で必要な桁数の解を求める策を採用
１．単位系と自然
力学で使われる量は質量、長さと時間が基本で、1kg、1m、1秒と我々が直接的に感じることができるため分かりやすいです。さらに、labo unitといわれる1g、1cm、1秒単位系であるCGS単位系への変換も単に1000倍と100倍で済みます。しかし、電磁気学となると電流という目に見えない量が出て来て途端に分かりにくくなってしまいます。
実用的には1940年代に決められたMKSA単位系（1m、1kg、1秒、1アンペア）から60年代に発展したSI（Le Système International d'Unités、国際単位）が用いられます。日常的に扱う対象物は、この単位系が好都合です。電磁気学では、力学と異なり、SI単位系とCGS単位系では、単なる100倍の様にはならず、さらに方程式の形も異なります。もちろん、次の節で説明するように、全ての物質は原子でできている訳で、それを基本とすれば原理的な統一は可能です。１アンペアの電流というのは、電荷e=1.6x10-19クーロンを持つ電子が１秒間に1019個流れたことを表しています。このような数え方をすれば、人間様の約束事が入る隙間はなくなりますが、電力会社への支払いを電子単位で行ったら、伝票の桁数がとんでもないことになってしまいます。そんなことをしないで済むようにしているのがSI単位系で、これも現場の知恵です。
逆にとてつもなく大きな値が出てくる天体運動を研究する場合は、天文単位（astronomical unit、AU）を使います。そこでは、地球が太陽の周りを回る楕円（だえん）軌道の長半径が1AU＝1.496x1011ｍとされ、この値を使うと木星の軌道半径は5.2AUとなり、地球より5.2倍遠方を回っていることがすぐに理解できます。
２．電子系の量子力学の方程式
電子系を記述するシュレディンガー方程式は、我々の世界のオーダーから遙（はる）かに小さい（例えば、電子質量meは9.1x10-31kg）世界を扱うため、原子単位（atomic unit、a.u.、天文単位と同じ記号！）を用いて記述することが多いです。原子単位は、一番小さい原子である水素原子を基本に考えます。質量と電荷は電子に対する実験値を単位として用います。水素原子は、陽子１個と電子１個からなる単純な系で、その挙動は量子力学の方程式を解くことで完全に解くことができます。例えば、その半径は（１）式の様に決まります。
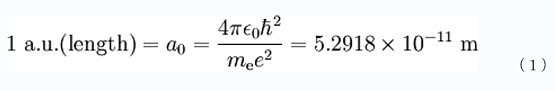
この値はmeを電子質量、eを電子の電荷、ｈをプランク定数として、数値的に求まっています。このように単位を設定することで、方程式は係数がほぼ１の大きさになり、数値計算の対象として扱いやすくなります。
ここで注意しなければならないことは、同じ名称なのですが、原子単位には２種類あり、ハートリー（Hartree）原子単位
と、リュードベリー（Rydberg）原子単位
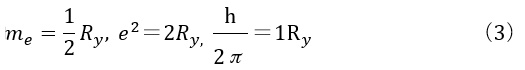
では、単位の大きさが２倍違っています。歴史的な事情が今でも続いており、量子力学の数値計算の現場では、このことを間違わないように常に慎重に数値を扱う必要があるのです。
３．流体力学の方程式
流体力学には、有名な「何とか数」と呼ばれる量が多く、例えばレイノルズ数、マッハ数、クーラン数、マランゴニ数、ペクレ数と、その物理現象を研究した研究者の名前を冠して呼ばれています。例えば、レイノルズ数（Reynolds number）
Re＝pUL/η （４）
は、流れ場の方程式を支配する無次元数で、流体の動的挙動を支配するナビエ・ストークスの方程式はReだけがパラメーターとなる無次元方程式に直せるため、この唯一の自由度であるReが同じ値なら、流れ場の解は等しくなることが知られています。ここで 、Uは速度、Lは長さ、 時間はL/U、圧力は U/Lで無次元化されます。Reが１より極めて小さい場合には、ストークス...
このように、流体力学では、物理的な方程式をそのまま解かずに、無次元化した方程式を数値的に解きます。電子系の量子力学方程式の原子単位と同等のことをしていることになるのですが、それによって誤差の算定も共通化でき容易になっているのです。
本稿で述べた様に、自然を記述する方程式を無次元化した方程式を数値的に解く場合、さらに、計算機の中では、全て有限の２進数で計算が行われていることを考えなければなりません。自然はその摂理に基づいて動的に変化していますが、それを数値的に解析する時は、スーパーコンピューターといえど未だに能力に限界があり、より現実的に有限の時間で必要な桁数の解が求まる方策を採用するのが現場数学の立場なのです。