♦ 単純そうに見え、実は奥が深い次元のお話
１．次元
空間には1次元、2次元、3次元とあり、時間も加えれば4次元があります。四次元空間といえば、タイムマシーンを思い浮かべる方も多いと思います。さらに、幾何学的にはいくらでも大きな次元も考えられます。「2次元空間を埋められる図形は三角形、四角形、六角形だけ、とずっと思っていたのに、五角形でも埋められる！」。イギリスの数学者ロジャー・ペンローズの考案した、2種類の菱形による非周期的空間充填は従来の常識を破りました。それが、3次元空間の等面菱形多面体による空間充填形を２次元空間に射影したパターンとして理解できることも驚くべき事実です。さらに、ペンローズタイルに対応した物質として、準結晶が発見され、彼の理論が単なる数学の玩具ではなく、自然に対応するものの存在を予言した素晴らしい理論であることが証明されました。
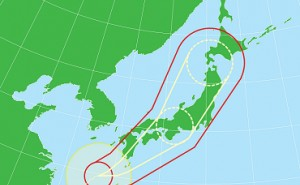
下図は、木工名人の中川宏さんが作成した3種類の12面体から構成される3次元物体ですが何と、4次元空間の正12面体の3次元空間への射影です。普通の正12面体を2次元平面に対称性よく射影すると、2種類の5角形（正5角形とひしげた５角形）が現れることはよく知られていますが、その延長なのです。
【写真説明】「多面体木工」NPO科学協力学際センター所蔵
２．半端な次元
4次元であろうが、５次元であろうが、次元が整数なことに違いはありません。しかし、世の中には1.26…次元なども存在するのです。小数次元と呼ばれます。それは次元の定義を、図形を半分にしたら何倍になるか？で定義することから始まります。線分を半分にすると、もちろん2個になりますが、正方形を同じ形に分けると4個になります。立方体なら8個です。分割された図形の数を2=21、4=22、8=23と表記し、指数部分をその図形の次元と定義します。これを相似性次元といいます。下のコッホ曲線を考えましょう。今度は線分を3等分するのです。真ん中部分を拡張して正三角形を作ります。次々とこの操作をしていくと…、1回に長さが元の4/3倍になりますので、どんどん増えて、無限回繰り返すと無限大の長さになります。有限の大きさの中に無限大の長さの線分が存在する、という不思議な結果なのです。
さて、コッホ曲線は、相似性次元の定義によれば、4=3dになりますから、d=log34=1.26…次元の図形です。普通に見える線分はいくら折れ曲がっていても1次元ですから、残りの0.26…次元は「見えないほど細かいシワシワ」の中にあるともいえるのです。
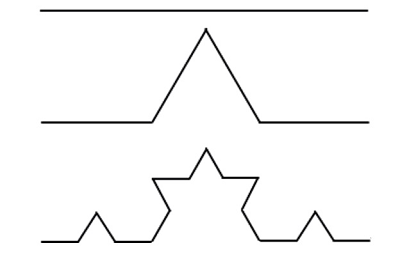
図1. コッホ曲線
３．フラクタルは現場にあふれている
「こんなものは、特別な数学の世界で、現場数学とは関係ない」と思ってはいけません。身の回りに、いくらでも半端な次元を持つ図形は存在しています。土木工事なら川の護岸工事。枝分かれした支流がまた枝分かれし、さらに小川になって……。小さい川でも数が増えるので、全体の長さを足せばとんでもない長さの護岸工事をしなければならなくなります。しのぶ石と呼ばれる酸化マンガンの結晶は、デンドライトとして知られています。水道などに発生する樹枝状晶もデンドライト形状になります。
リチウム電池が火災を起こした原因もデンドライトの発生にありました。下の図がデンドライトのパターンですが、これは計算機で簡単に作成できます。
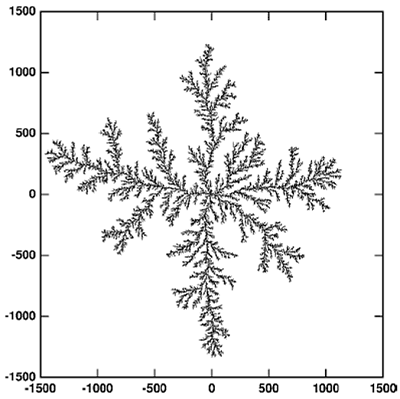
図2. デンドライトパターン
真ん中にある大きさの初期位置を設定し、適当...
一見、単純そうに見えるのに奥が深い。これ現場数学では、常に注意しないといけないことそのものです。