【工程能力の理解 連載目次】
前回のその2に続いて解説します。DPMOとはDefects Per Million Opportunityのイニシャルを表し、百万機会当りの欠陥数と言う意味になります。ここで言う機会とは欠陥をチェックする機会を指します。DPMOは百分率%と同様に百万個あたりの欠陥数と同義で用いられることもありますが、正確には異なります。例えばある製品の最終検査項目が5項目あれば、製品一個当りの検査機会は5となります。1機会当りの欠陥数はDPO(Defect Per Opportunity)と言い、5回のチェックで1箇所に欠陥があれば、DPOは1/5=0.2となります。
1機会当りの欠陥数DPOが分かればこれを百万機会に換算するとDPMOを求めることが出来ます。上記の例で言えばDPMOは0.2x1,000,000=200,000です。ではこの製品10個を同様に検査して、欠陥が1箇所であればDPMOはいくつになるでしょうか?
【DPMOの計算例】
上記のようにまずはDPOを求めます。欠陥数は1ですから、機会数を求めればDPMOも容易に算出できます。単純に機会数が10倍になっているので0.1を掛けても求まります。しかし統計的には工程能力が6シグマに相当するDPMOは0.001ppmと極めて低く、3.4ppmに相当するシグマ値である4.5とは異なります。この理由の解説も含めてDPMOとシグマレベルの関係を解説します。
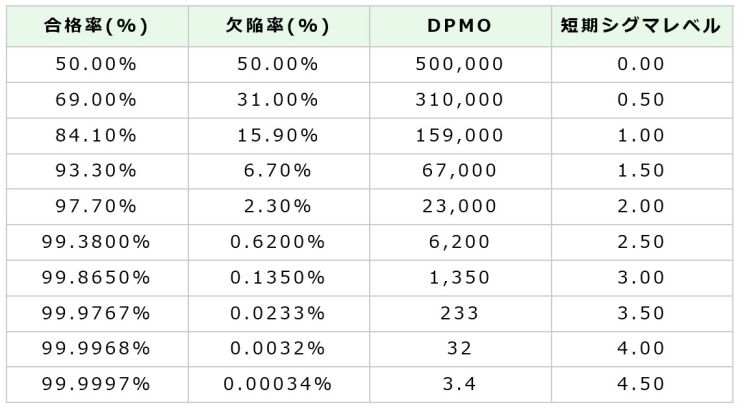
欠陥率が50%であれば100万機会当りの欠陥数は50万個となり、DPMOは50万ppmとなります。欠陥率を標準偏差が1(σ=1)の標準正規分布で表すと、欠陥率、DPMO及びシグマレベルの関係は図1の様になります。
図1.欠陥率、DPMO及びシグマレベルの関係
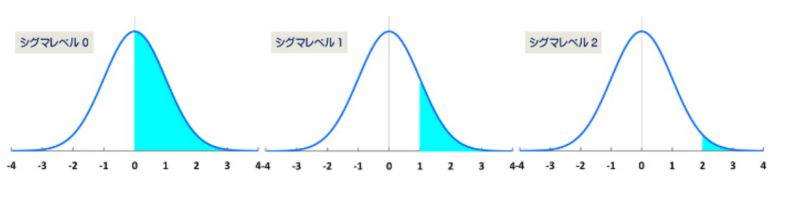
この場合の欠陥率とシグマレベルを標準正規分布で描画すると、図2の様になります。水色でカラーリングしている部分が欠陥率です。シグマレベル0の時はDPMOは百万の半分の50万であり、半分が欠陥である事が図から読み取れます。
図2.DPMOと短期シグマレベルの関係
上表記載の合格率や欠陥率から、エクセル関数を用いてシグマレベル及びDPMOを求める式は以下の通りです。エクセル関数はエクセル2010版を用いています。これ以前のエクセルの場合はnormsdist関数やnormsinv関数を用いれば同様に求められます。
歩留りからシグマレベルを計算する式
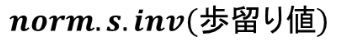
シグマレベルを用いて欠陥率を計算する式
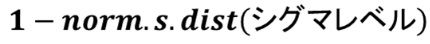
シグマレベルからDPMOを計算する式
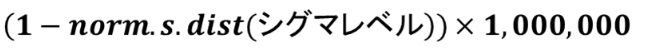
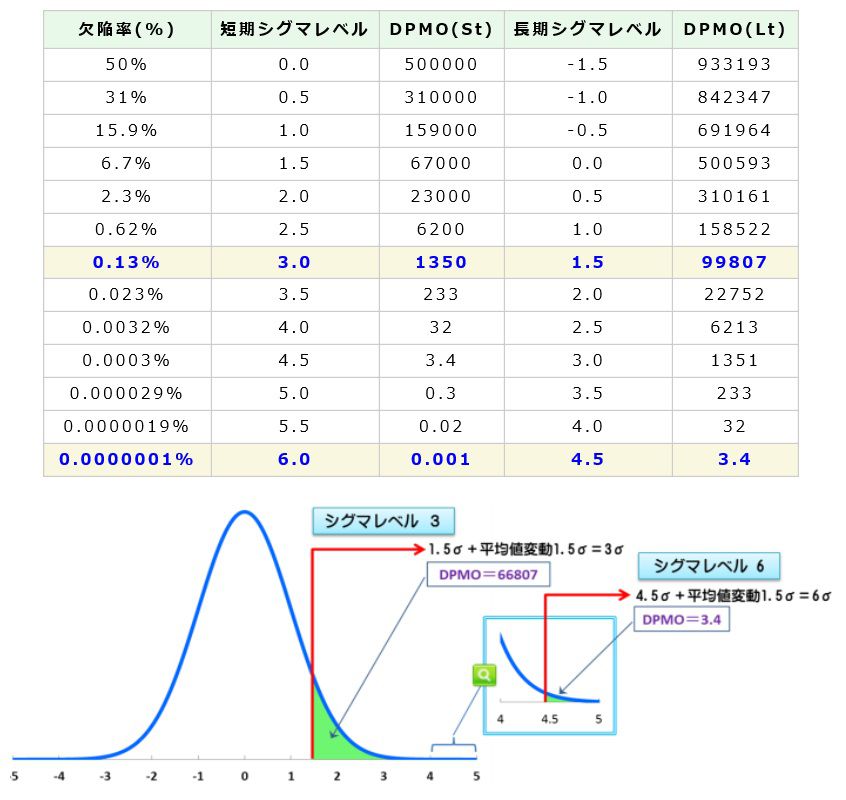
DPMO算出に用いたデータが、一定期間(短期間)で採取されたものである場合、長期工程能力は短期工程能力よりも低下します。平均値のシフトや分散の変化が生じるためです。経験則的に長期性能は短期性能よりシグマレベル1.5シグマ分低下すると言われています。即ち短期収集データでシグマレベル6相応の工程能力があれば、長期ではシグマレベル4.5として捉えます。DPMOも同様に4.5相当のDPMOとして見なされます。故に4.5に相当するDPMOは3.4ppmとなり、シックスシグマのスローガンと一致します。(図3)
図3.DPMO(St)(Lt)
...