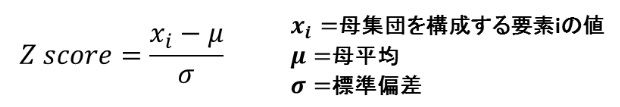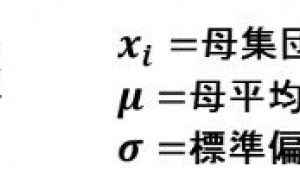【工程能力の理解 連載目次】
今回は、その4として、Zスコアと標準化を、4回連載の工程能力の理解の最後として解説します。
1. 工程能力・工程能力指数とは
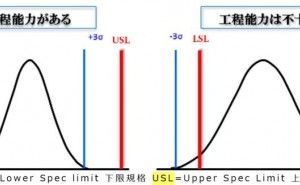
特性値の規格に対する充足度を工程能力と言います。工程により作り出される特性の状態を評価するには平均値だけでは不十分で、母集団のばらつきを考慮した分布の大きさを観る事が重要です。この分布が、規格(スペック)幅の内側に十分収まるように管理を行う事が、品質保証に直結しコスト削減と顧客満足に繋がります。
工程能力とは安定した工程における品質特性値の状態を、統計的に表す能力の事を言います。ここで言う安定した工程とは、簡単に言えば特性の異常なばらつきが無い状態と言えます。管理図で言えば管理限界内で点が、特異な傾向無く上下している様なケースになります。設備の故障や人為的ミス、その他平常時とは異なるイベントによる異常を含まない状態です。
その2の復習になりますが、スペックに対し特性の分布がどの程度余裕を持って納まっているかを知る為の指標が、工程能力指数です。特性値の中心を決めるのが平均値とすれば、分布の範囲を決めるのが、ばらつきといえます。 この場合ばらつきは標準偏差σを基準として算出されます。
平均値と標準偏差を用いて工程能力を分かりやすく指数化したものが”工程能力指数”です。 一般的にCpの記号で表記されますがこれは、Process Capabilityの頭文字を取ったものです。
2.Zスコアとは何か
前回のその3に続いて解説します。Zスコアは、ある値xiが分布の中でどの辺りに位置するかを平均値0、標準偏差1の標準正規分布に置き換え表したものです。Zスコアは下の算出式で導く事が出来ます。
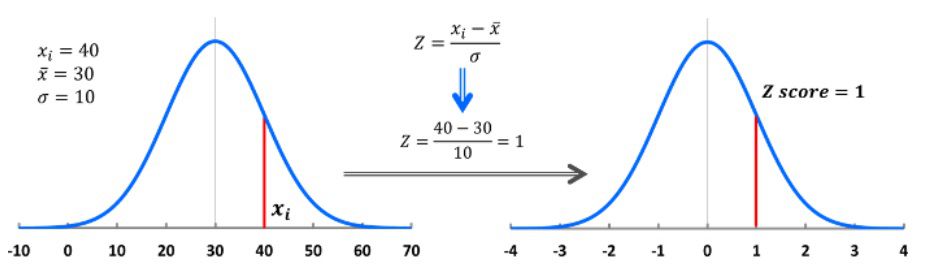
xiが平均値と等しければZスコアは0となり、平均より高い値ならZスコアはプラスの値、低ければマイナスの値となります。このZスコアを求める式は、標準偏差の値が異なる分布を、標準正規分布に置き換えたものと考えることが出来ます。例えば上限規格値が40で、平均値30、標準偏差10の正規分布を計算すると図1の様になり、Zスコアは1となります。
図1.標準化イメージ
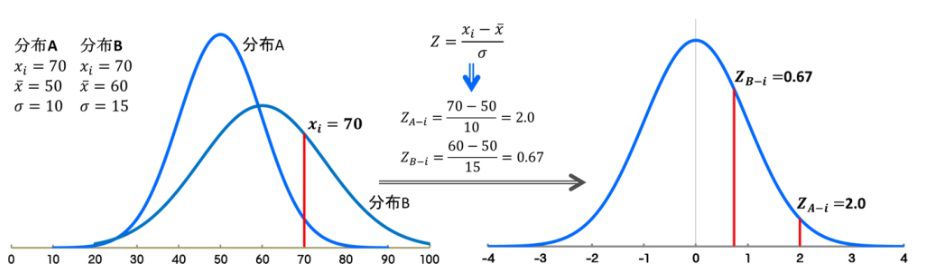
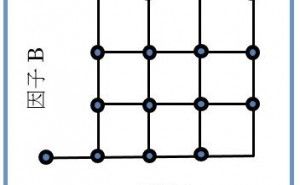
Zスコアを用いる利点は、平均値や標準偏差が異なる分布の値も、標準正規分布という同一分布の中の値として比較が可能な所です。例えば数学と英語の成績の良し悪しは単なる点数の比較では判断できません。同じ70点でも点数の分布の平均と標準偏差によって分布のどの辺に位置するかが異なるからです。数学の平均と標準偏差が50点と10点(分布A)で、英語の平均と標準偏差が60点と15点(分布B)だとすれば、70点の結果のZスコアは、図2のように、数学が2.0、英語は0.67となります。
図2.異なる2つの分布の標準化イメージ
因みに両試験における70点を偏差値に表すと、それぞれ数学は偏差値70、英語は偏差値60相当となります。偏差値70は1000人受験者がいれば23位付近であり、60は253位付近となります。
3.Zスコアの応用 偏差値
学力を表す統計指標に偏差値がありますが、これもZスコアと同様に標準化指標です。偏差値は分布の平均が50となり、50<の場合は平均より成績が上位で、50>は成績が下位である事を示唆します。偏差値はZスコアを用いる事で次の式にて容易に求める事が出来ます。
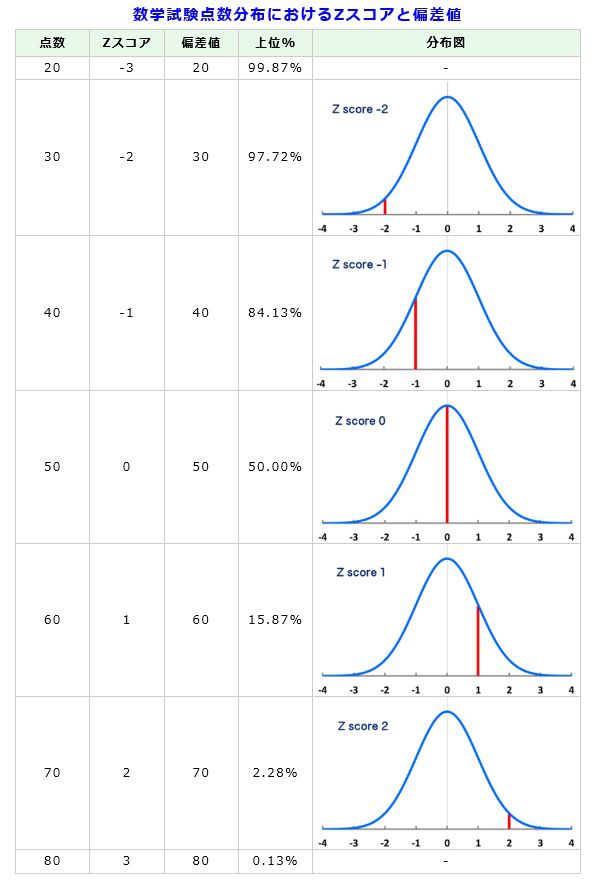
数学の点数分布において、Zスコア及び偏差値をZスコア分布と共に図3に示します。また各Zスコアが上位から何%に相当するかも併せて記します。
図3.数学試験点数分布におけるZスコアと偏差値
Zスコア2若しくは偏差値70は上位2.3%に入る...