電気エンジニアから「直列に接続した抵抗の誤差(tolerance)」についての質問を受けました。なんでもその電子回路は重要なフィードバック回路で、高い精度が必要にも関わらず、コストをかなり下げなければならないそうです。そのため誤差 0.05% などの高精度の抵抗は使えず、安い汎用の誤差 1% や 5% の抵抗などを直列で使いたいというものでした。そこでそのエンジニアは「抵抗を直列に接続した場合、その誤差はどのようになるのか」と疑問を持ったわけです。
僕の回答は、次の4点です。
- 誤差の値を最悪値(ワースト・ケース)と定義した場合は、直列に抵抗を接続しても誤差の値(%)は変わらない
- しかし、実際に最悪値の抵抗が使われる確率はかなり低い
- しかも直列に接続された抵抗のすべてが最悪値の抵抗である確率はもっと低い
- 従って、抵抗を直列に接続した方が精度も上がるし、コストも下げられる
そして、この理由を説明したときに「これは
DFSS(Design for Six Sigma)の考え方を説明する良い例だな」と思ったので、今回は、この事を掘り下げて、解説します。
1. 従来の決定論的なアプローチ
電子回路の設計に限らず、従来の意思決定の多くは典型的な値をもとに判断します。たとえば平均値だとか、誤差の場合は最悪値(ワースト・ケース)といった特定の値を使います。これは決定論的(Deterministic)なアプローチといわれます。
直列抵抗の誤差は、決定論的なアプローチを使った場合は、単体の抵抗であろうが、複数の直列抵抗であろうが、誤差の値(%)は変わりません。簡単な計算をしてみれば分かります。誤差 1 % の 1000 オーム抵抗を考えてみます。誤差は 1 % なので、1000 オーム抵抗といっても、実際には 990 オームから 1010 オーム まで幅があることが分かります。
これを同じく誤差 1 % の 100 オーム抵抗を 10 個直列して作るとします。最悪値(上限)の場合、101 オーム抵抗を 10 個使うことになります。そして最悪の合計抵抗値は、1010 オーム( 10 * 101 オーム)となり(下限値は 990 オーム)、誤差の値は単体の抵抗も、複数の直列抵抗も、まったく変わりません。
2. 確率論的なアプローチ
統計を使う DFSS(Design for Six Sigma)やリーンシックスシグマは、確率論的(Probabilistic)アプローチをとります。上記の例だと、「では、最悪の抵抗が連続して 10 回使われる確率はどのくらいか」と考えるわけです。
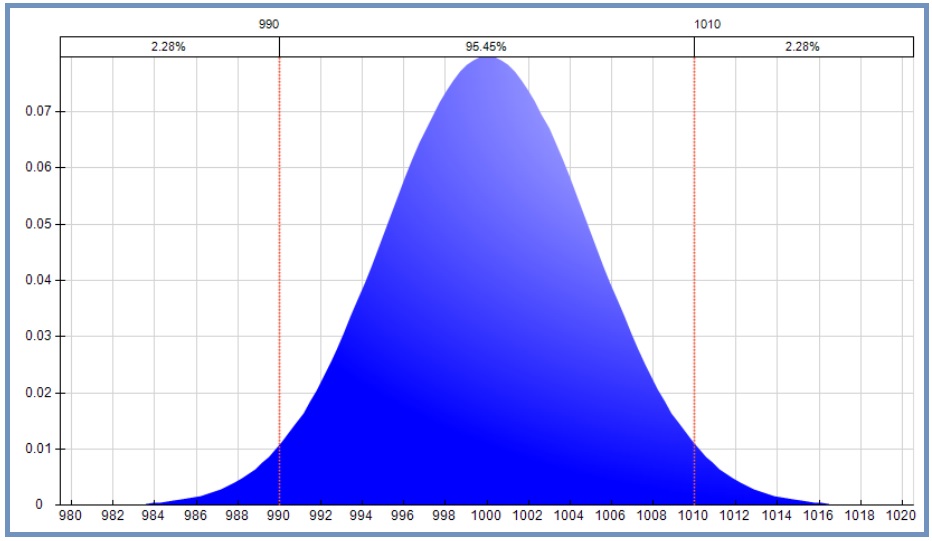
メーカーから大量に購入する抵抗の抵抗値は、だいたい正規分布をとることが分かっています。仮に 2 シグマ(標準偏差)が誤差の範囲とすると、誤差 1 % の 1000 オーム抵抗(単体)の分布は図のようになります。
つまり 990 オームから 1010 オーム(± 2 シグマ)に間に、購入する抵抗の 95.5% が収まることが分かります。逆に言えば、最悪な抵抗を使う確率(片側)はたったの 2.25 % しかありません。抵抗単体の場合でも最悪値の確率(片側)は 2.25 % しかないのに、10 個の抵抗が連続して最悪値の場合はどのくらいあるでしょうか。0 % ≒ 2.25 % の 10乗誤差 1 % の 100 オーム抵抗を 10 個直列して 1000 オームを作った場合、その誤差が 1% になる確率はまずないと言っても良いでしょう。
3. モンテカルロ・シミュレーションで確認
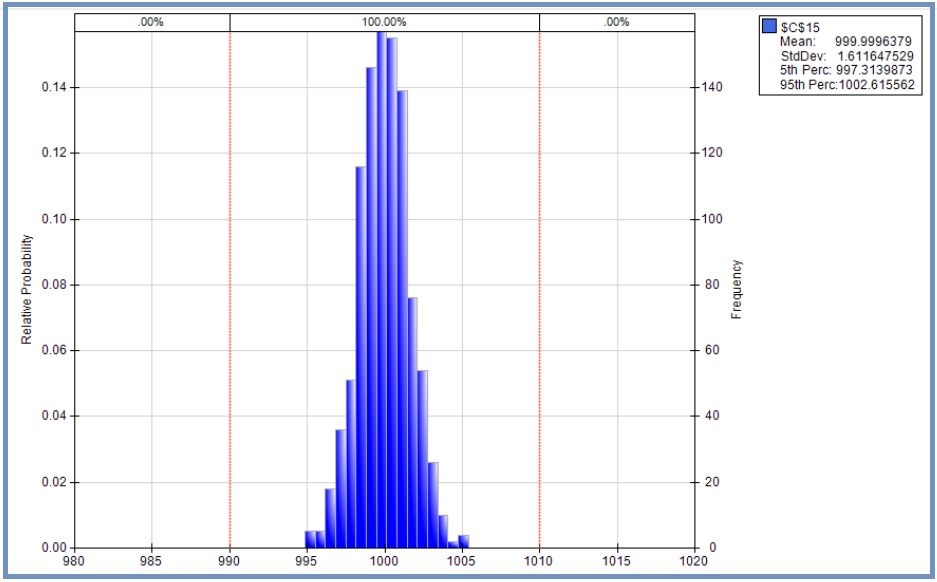
「誤差 1 % の 100 オーム抵抗を 10 個直列する」という簡単なモデルを使ってモンテカルロ・シミュレーションをした結果、以下の結果が得られました。
抵抗値が 990 オーム以下または 1010 オーム以上になるということがほとんどないことが分かります。またシグマ(標準偏差)が 1.61 オームなので、「 2 シグマ(標準偏差)が誤差の範囲」という定義を使えば、この直列抵抗の誤差は 3.22 オーム、つまり誤差 0.322 % となります。
4. ランダム・サンプル
ここでひとつ問題があります。上記のような確率論的なアプローチは、ランダムなサンプルを前提にしていることです。
もし抵抗の選定がランダムに行われていれば、確率論的なアプローチは決定論的なアプ...