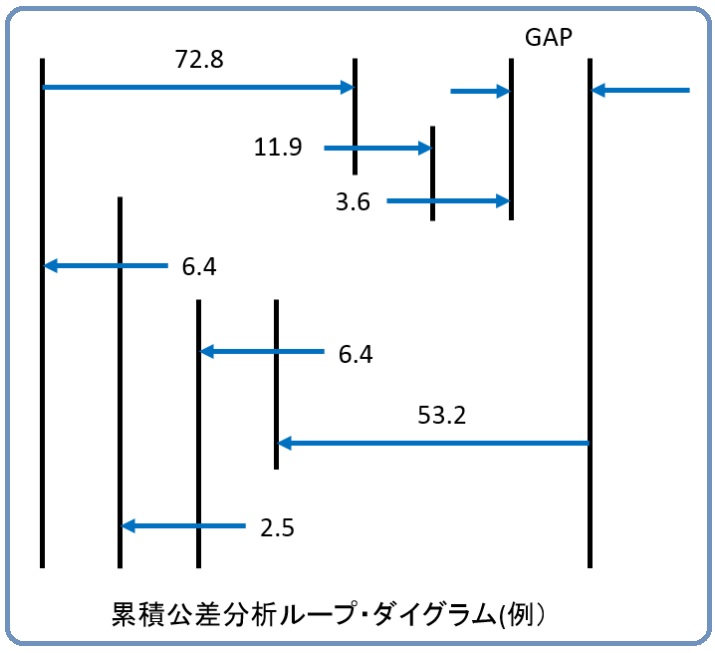
先日、ある質問を受けました。質問内容は、「射出成型機を使って製作する 4 つの部品を設計する際、その4つの部品がちゃんと組み合わさるためには、リーンシックスシグマを使ってどのように品質管理をすればよいのか」というものでした。それを聞いて、典型的な累積公差分析(Tolerance Stack-up Analysis)の質問だと思いました。以下は、質問に対する僕の答えです。
1.モンテカルロ・シミュレーション
設計段階では部品には誤差がないので、設計に誤りがなければ、問題なく部品を組合すことができるはずです。しかし射出成型機を使って製造された部品には一つ一つ違った誤差が出てきます。ある時は設計値よりも幾分小さく、またある時は逆に幾分大きかったりします。その誤差の範囲を公差( Tolerance)と呼んでいます。部品設計の際は、それぞれの部品に公差があっても、上手く組み合うように設計しなければなりません。
質問のケースでは、部品が 4 つだけなので、公差の最大値や最小値の組み合わせも比較的簡単に考えることができるかもしれませんが、部品点数が多くなると、すべての部品の公差を含めた組み合わせを考えて設計することはとても困難になります。そのためシミュレーションを活用することになります。
累積公差分析で良く使われるツールが、モンテカルロ・シミュレーションです。モンテカルロ・シミュレーションは、シミュレーションする対象(数値モデル)の入力値を公差の範囲内の乱数として、その乱数を使って何千回も計算することにより、その出力値の分布を調べるものです。
モンテカルロ・シミュレーションによって、部品を正しく組合すことができない場合の確率が分かります。仮に、0.1 パーセントの確率で部品を上手く組合すことができないとします。その 0.1 パーセントをどのように考えれば良いのか、コスト掛けて部品の製造精度を上げる(公差を小さくする)か、または製品を安くするために、その程度の不良品は良しとするか、などモンテカルロ・シミュレーションは設計基準などを決める材料を与えてくれます。
モンテカルロ・シミュレーション用ソフトウェアはたくさん市販されていますが、乱数機能を使えばマイクロソフト・エクセルだけでもモンテカルロ・シミュレーションを行うことができます。
2. 許容分析(Capability Analysis)
モンテカルロ・シミュレーションでは不良品(上手く組み合わない)の確立が 0.1 パーセントなのに、実際の不良品の確立はもっと高かったとします。恐らく、実際に製造される部品の公差が、設計時に計算した公差よりもはるかに大きいのだと思います。それを調べるには実際に製造された部品の大きさを調べて(サンプリング)、統計的に解析する必要があります。
サンプリングした部品の大きさをヒストグラムで表すと、部品サイズのバラつき(分布)の様子が分かります。射出成型機で作った部品は、恐らく Weibull 分布だと思います。その分布をもとに、実際の不良品の確率やシグマレベル(Z-score)を、許容分析を使って求めることができます。
モンテカルロ・シミュレーションと同様、許容分析は製造上の問題対策の考える基準を与えてくれます。
3.工程管理
製造された部品のロットによって品質にバラつきがあることがあります。あるロットは品質が高く、すべての部品が公差内に収まっているにも拘わらず、違うロットでは不良品が多い、という様な場合です。
そのようなロットによる品質のバラつきは、定期的な部品のサンプリングによって、検出できます。各種のコントロール・チャート(Run、Xbar-R、XBar-S、など)を使えば、そのパターンによって製造過程で何が起こっているのかを推測することができます。
4. 原因分析
シックスシグマには問題の原因を特定するためのツールが沢山あります。Fishbone分析図、5Why、C&Eマトリックスなど、たくさんあります。状況に応じて適切なツールを使って根本的な問題の原因を探します。
5. DOE(Design of Experiments)
問題の原因が分かっても、それが実際にどのように部品の製造誤差につながるのか、それが分からないことがあります。例えば射出成型機の場合は、材料の温度、型の温度、材料の注入速度、材料の質、など色々な要素が複雑に絡み合って部品の精度が決まってきます。問題を解決するためには、それぞれの要素がどのように最終的な部品の精度に影響しているのかを調べる必要があります。
そのような場合、リーンシックスシグマでは DOE(Design of Experiments)というテクニックを用います。
DOE には、スクリーニング DOE と モデリング DOE の2つの過程があります。まずスクリーニング DOE ...