【この連載の前回：計測の精度と不確かさとは（その4）不確かさの定義へのリンク】

測定の”不確かさ”という従来の“精度”に置き換わる概念が「世界中のどこでも共通の定義で扱える量」「計算や表現が規定される量」として、1993年以来ISOで提案され、国際規格や論文等の技術基盤として浸透しつつあります。前回に続けて今回は、測定の不確かさの具体的な計算方法について解説します。

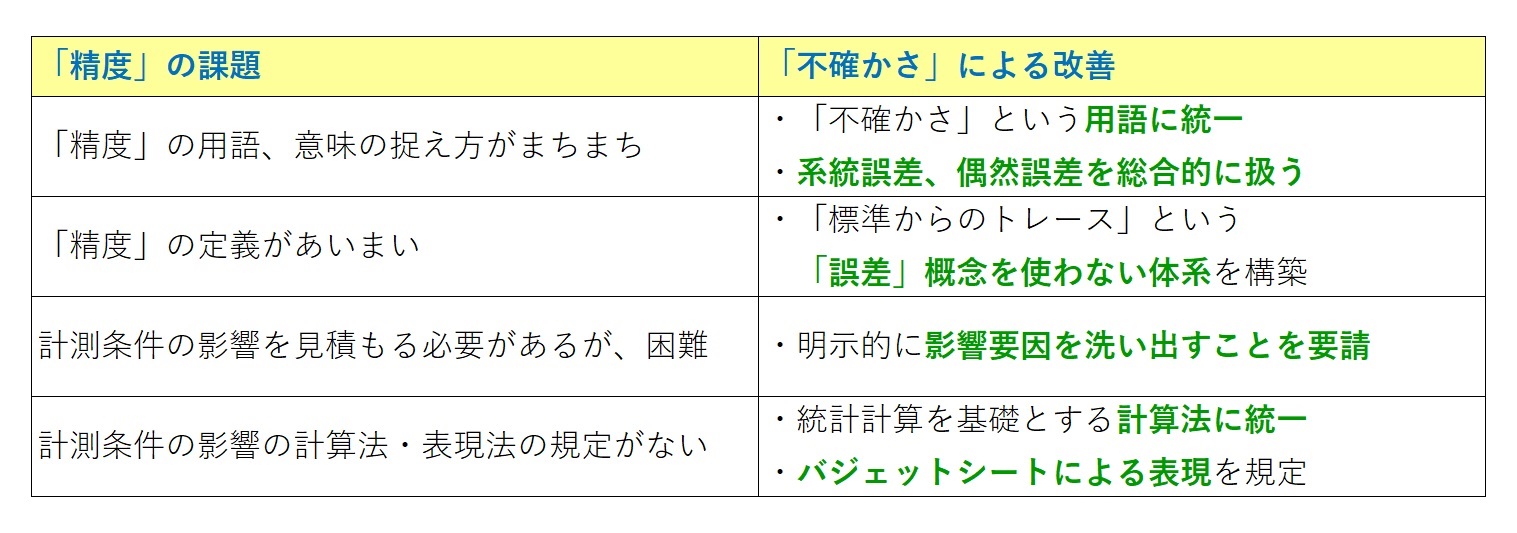
5.「不確かさ」の計算・表現方法

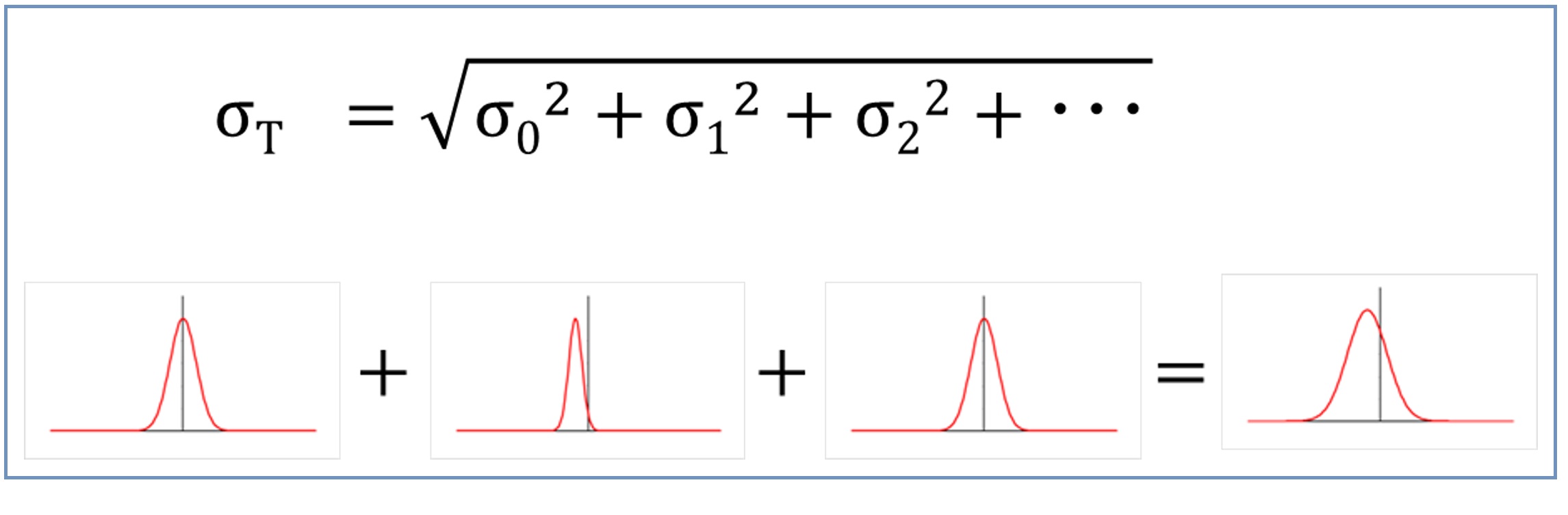
不確かさの計算方法を、以下に順を追ってご説明します。先にご説明しましたように不確かさは計測で発生するばらつきを表していますので、計測時にばらつきを発生させる要因をすべて洗い出し、各要因に起因して発生するばらつきを加算することで全体としての計測結果のばらつき＝信頼度を計算するという流れになっています。

(1) ばらつき要因の洗い出し

センサ・計測器自体のばらつきや、計測条件による影響要因を全てリストアップします。ここで全ての要因について網羅性することが計測の信頼性の担保につながるため、全体の中のベースとなる番重要な手順となります。そのためには、図4のように4W1Hで考えを見える化、識者を交えたブレインストーミング、部署内でのレビュー等により検討漏れ防止を行うことが効果的です。

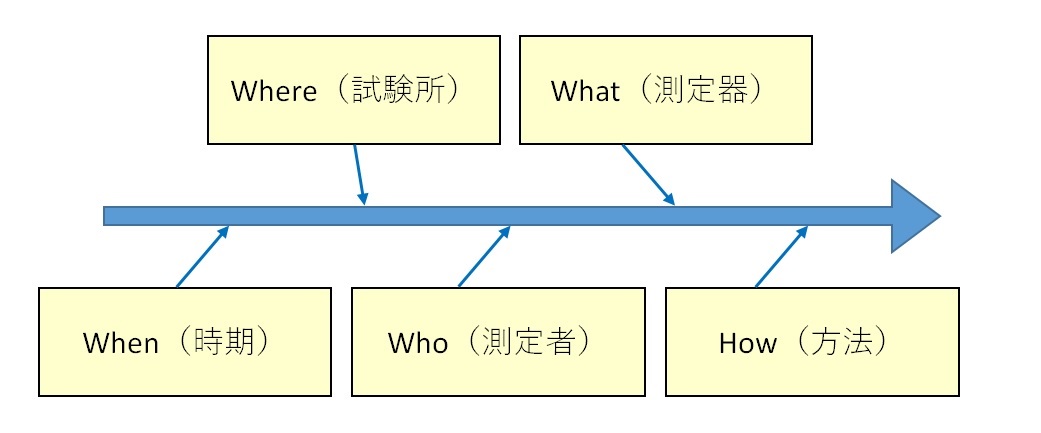
図4.要因の分析

(2) 要因毎にばらつき（標準不確かさ）を見積り

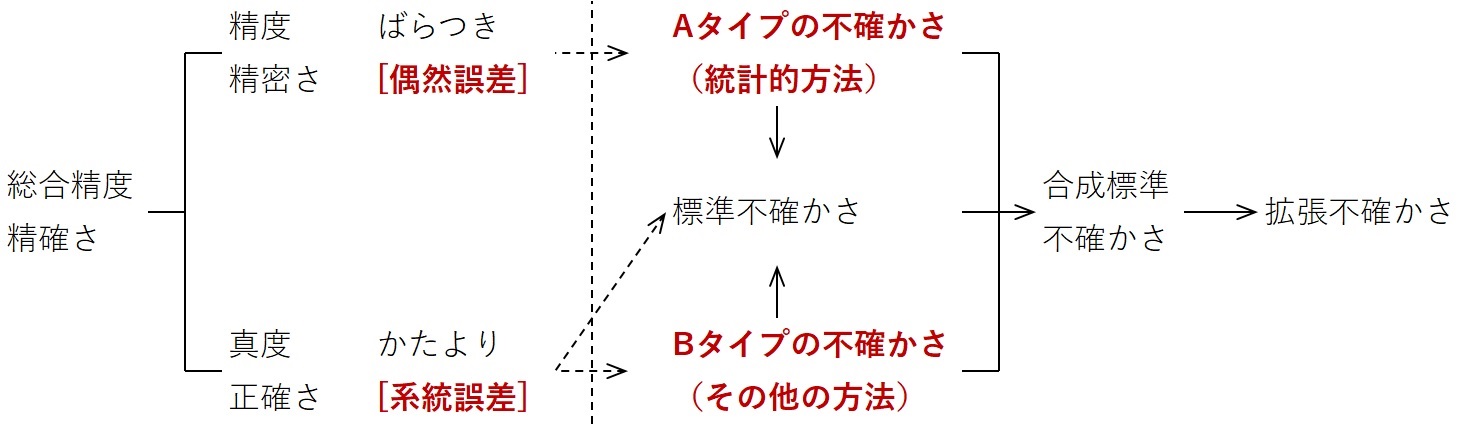
次に、挙げられた各要因でどの程度のばらつきが発生するかを定量的に見積もる手順になります。その際、次の2つのどちらかの方法を用いますが、それぞれに得失がありますので状況に応じた適切な方法を選びます。

• タイプA：統計的方法によって評価（繰返し測定でばらつきを実測）直接的だが、測定値に含まれる複数要因の影響を分離するのが難しい
• タイプB：その他の手段で評価（校正データ、カタログ値など）単独影響を求められるが、根拠の調査や推定の要素が含まれる

また、ばらつきの分布の形は基本的に正規分布で考え、例えば計測分解能の範囲内のように値が一様に存在する可能性がある場合は矩形分布とする等、分布形状についても合わせて検討を行います。

(3) 標準不確かさを合成（二乗和計算）して合成標準不確かさを計算

次に、集められた各要因によるばらつきを合成する手順になります。合成の計算は統計計算に用いられる二乗和計算で次式のよう行います。この時、ばらつきが正規分布でない場合は、事前に標準偏差と等価になるσiの値に修正を行います。（図5）

図5.不確かさの合成

(4) 包含計数を加味して、拡張不確かさを求める。

計算されたσTは統計計算の標準偏差に当たりますので、実際の分布範囲を求めるために包含係数（通常はｋ＝2）を乗じて、拡張不確かさの範囲を計算します。①～④のプロセスを図6に示します。

図6.ばらつきの見積り方法
＊南 茂夫、木村一郎、荒木 勉「はじめての計測工学」を参考に作成

(5) 計算結果を不確かさ成分のバジェットシートとしてまとめる

以上の計算結果を表（バジェットシート）まとめ、検討した要因とそれぞれの量が見えるようにします。（図7）

図7.不確かさ成分のバジェットシート（例）

6. 校正、トレーサビリティ

現在、国の計量関係の校正体系（トレーサビリティ）は、これまで説明してきた不確かさの考え方を使って図8のように構成されています。ここで、下位の標準器の校正は、上位の標準器に値付けされている不確かさに自身の校正作業で生じる不確かさを加えることで行われています。こうして最上位の国家計量標準から下位に行くに従って不確かさを加えていき、自身の標準器または計量器の不確かさが分かるようになっており、一般の使用者はこの不確かさが与えられた計測器を用いることで、自身が行っている計測の不確かさの基準が与えられることになります。

図8.トレーサビリティ
＊今井秀孝「測定不確かさ評価の最前線」を参考に作成

7. まとめ

測定の“不確かさ”の計算により、“精度”をベースにすることによる課題が解消し、国際レベルで統一された基準で計測値の信頼性を評価/表現する指標が手に入ることがご理解頂けたと思います。このことは、単に計測結果の信頼性が担保されるだけではなく、使い方によっては「製造ラインの検査能力が把握されることで検査条件が緩まり歩留まりが改善される」といった多くのメリットを得ることにもつながります。

表4.精度と不確かさの比較

ただし、実際に運用してみると、計測についての広範な深い知識・スキルが必要であり計算に自信が持てない、要因が膨大で計算に非常に多くの手間・時間を要する等の理由で、全ての場面で使うには障壁があることが分ってきます。そのため、運用に当たっては次のように用途や計算を適用するレベルを調整して使うのが現実的と考えます。

• 校正などの厳密性を要する用途で使う
• 一般試験で、影響が大きい要因に絞って計算する

因みに、GUM(Guide to the expression of Uncertainty in Measurement)の中でも次のように書かれており、不確かさの評価が大きく「人」に依存していることを認めています。このことからも分るように、完全性を追求するのではなく、むしろ自社の技術力を示す一つの強力な手段ととらえ、有効に活用していって頂きたいと考えます。

（GUM（3.4.8））^[2]から『不確かさの評価は、測定量や測定の性質についての知識の詳しさに依存する。測定の結果に付けられる不確かさの質と効用は、その値付けに携わる人々の理解、鑑識眼のある解析、そして誠実さにかかっている。』

【参考文献】
[1].ISO/IEC Guide 99：International Vocabulary of Metrology（VIM）国際計量計測用語)：計量に関する国際的な用語集
[2].国際文書「GUM(Guide to the expression of Uncertainty in Measurement)」（ISO guide 98-3としても位置付けられている）