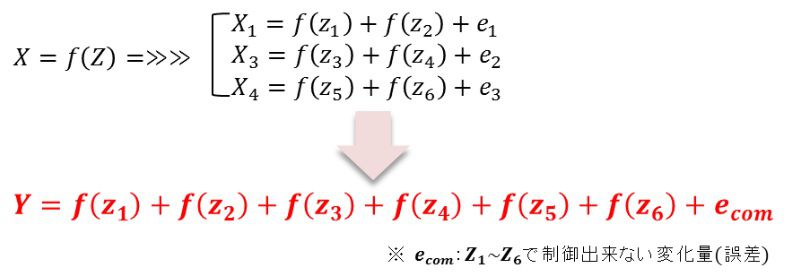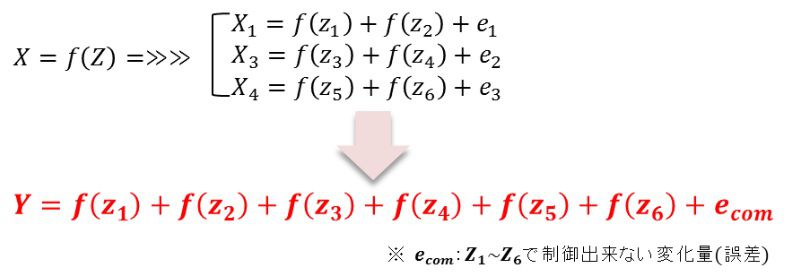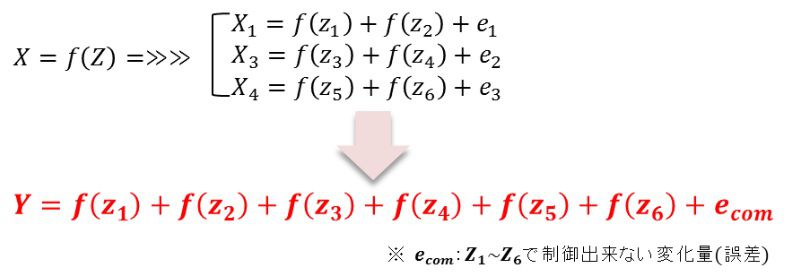前回のその6に続いて解説します。Improveフェイズでは、特性Yと、Analyzeフェイズの最後で抽出した影響力の大きい要因Xとの関係を伝達関数とします。Yは、主要な要因Xの変化で決まるという考えに基いており、要因Xを制御する事で実際にYの改善効果が観られるか検証していきます。
・Improveフェイズの、取り組み。
1. Y=f(x)関数の構築
2. Y=f(x)関数のXの制御範囲を決定する
3. 検証実験を行いYの改善を確認する
Yは、問題を解決するための改善指標であり、XはYに影響を与える要因を表します。f(x)は全ての要因xの、Yに対する影響の大きさ(寄与度)を表しています。要因X全てを管理するのは効率が悪いので、効果が低い要因は誤差と見なし、効果の大きい要因の制御に注力します。
1.Y=f(x)関数の構築
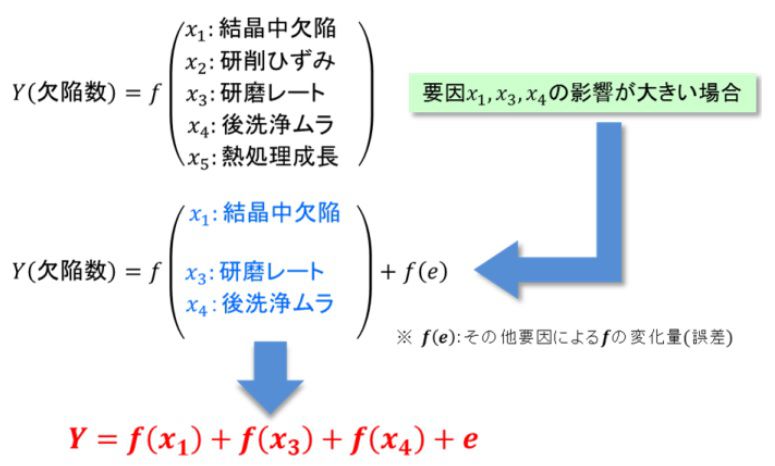
特性Yを欠陥数、Xを欠陥に影響する製造要因とすると、Y=f(X)の関係は図1の様に考える事が出来ます。因みに要因Xがn個の場合、Y=f(x1,x2,x3,・・・xn) と表されます。Yのばらつきに著しい影響を与える要因がX1,X3,X4の3つであれば、Yは要因X1,X3,X4の効果f(x1,x2,x3)とその他の要因全ての効果(誤差e)で表す事が出来ます。
図1.特性Yと要因Xの関係
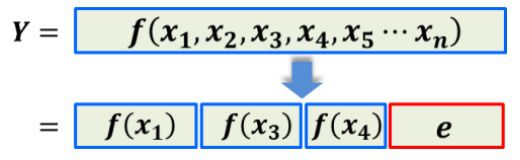
上式は特性Yは、主にx1,x3,x4の3つの要因と、その他誤差要因で決定するという意味で、厳密な数学公式とは異なります。因みにYに与える影響が大きい順にX1⇒X3⇒X4であるなら、Yを構成するf(xn)と誤差の大きさイメージは、図2のような感じとなります。
図2.特性Yと3つの主要因との関係
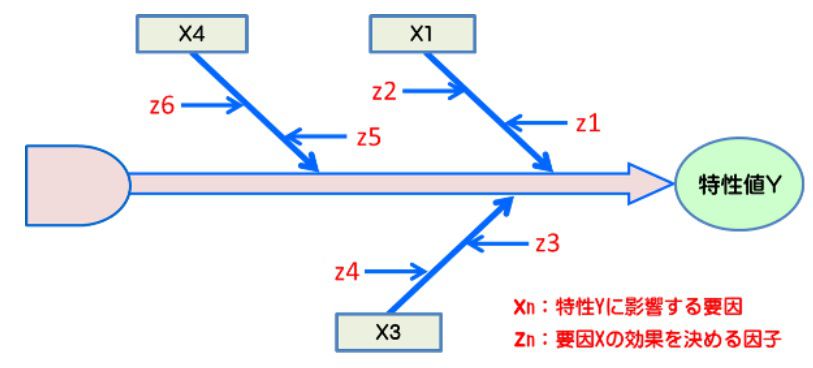
Yと複数の要因xの関係は、実際に対応したデータを解析する事により、回帰式の形で近似する事が出来ます。但し、実際の現場では要因xを直接制御出来ないケースもあり、この場合要因Xを制御するための因子zを制御し、間接的にYをコントロールします(図3.参照)
図3.特性値Yの要因XとXの効果を決める因子
例えば、事例のX3は研磨レートですが、研磨レートが砥液流量(z1)と研磨時間(z2)で決まっているなら、z1とz2を制御する事で間接的に欠陥数Yもコントロール出来ます。同様にX3とX4に対応している因子z3~6を制御する事でも、Yをコントロール出来ます。即ち、Yを制御する伝達関数は要因Xを制御する因子Zを用いて次の様に表すことが出来ます(図4)
図4.伝達関数
2.Y=f(x)関数のXの制御範囲を決定する
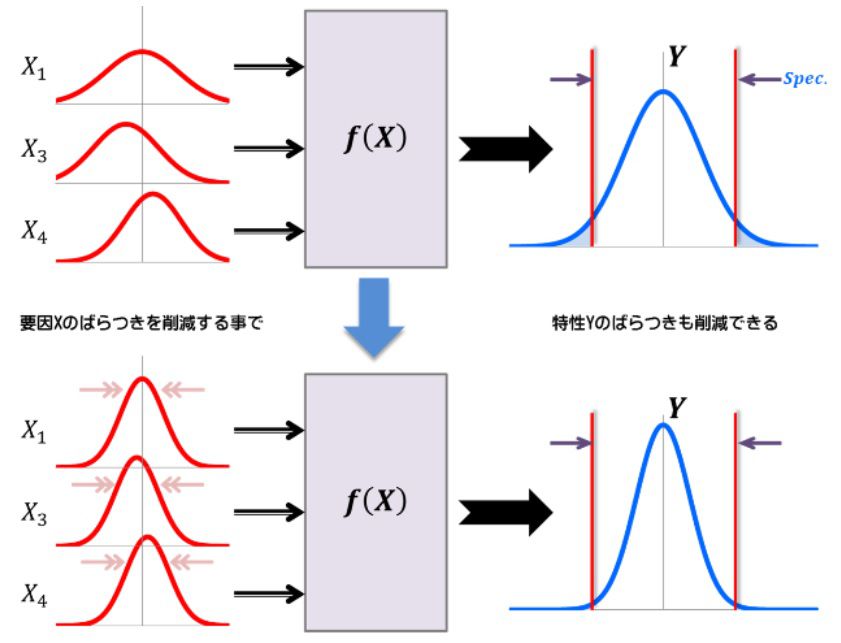
Yの変化の大半を、要因X1,X3,X4で説明出来るなら、これら主要因を一定の範囲に制御する事で、Yの分布の抑制も可能と考えます。即ち、顧客が要求する規格範囲の中に、Yの分布の大半が十分収まるようなXの可変域を決定します(図5)
図5.伝達関数イメージ
要因X(インプット)の制御と特性Y(アウトプット)のイメージは、図5の様になります。Xの分布を管理する事で、間接的に特性値Yの工程能力を改善する事になります。つまりY品質を管理する為に、主要因Xの管理を徹底する必要がある事を説明しています。
図5の伝達関数イメージは、特性Yを要因Xでコントロールする場合ですが、特性Yが要因Xを支配する因子Zで制御できるなら、同様にYを規格範囲に収めるために、Zの可変領域を決定します。
3.検証実験を行いYの改善を確認する
特性Yを改善する為の条件が整えば、それが効果的に機能するかどうか検証作業を行います。伝達関数の仮説が立てられれば、それが成り立つかどうか、統計的仮説検定や推定、分散分析法などの手法を用いて確認します。
検証データ数が稼げるようなら、短期性能の工程能力を算出し、改善前と比較します。検証の結果、期待した効果が得られないようなら、状況に応じ...