前回のその1に続いて解説します。
5. D/O(Design and Optimize/設計と最適化)フェーズ
Design and Optimize フェーズでは以下のツールを使いました。
- Boundary Diagram
- Cause & Effect Diagram (Fish Bone Diagram)
- Parameter Diagram (P-Diagram)
- Design FMEA
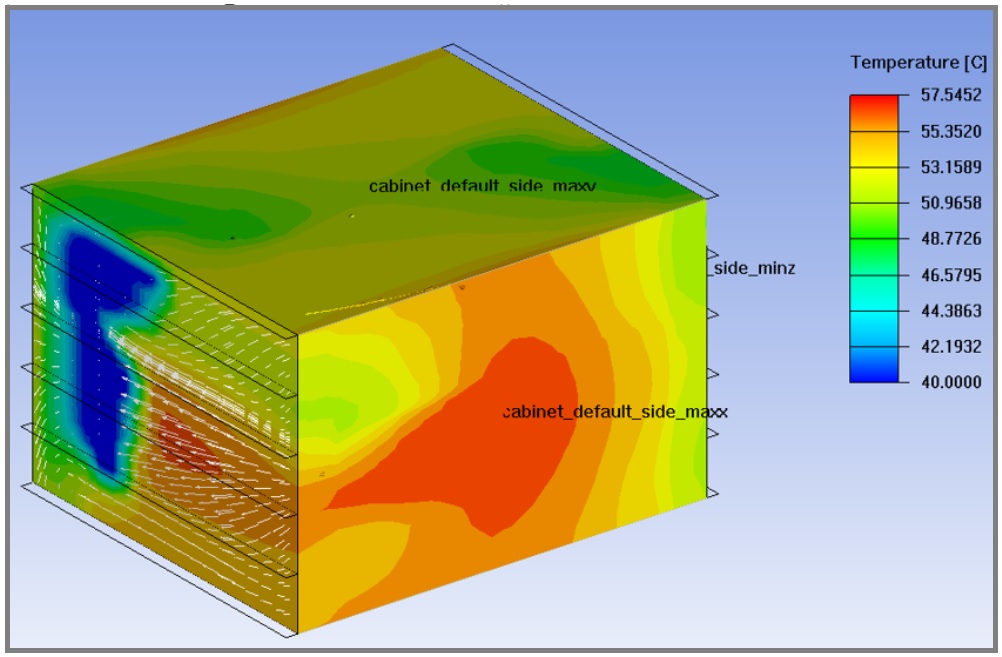
- Thermal Modeling (熱計算のための数値モデル)
- モンテカルロ・シュミレーション
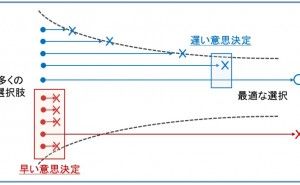
このグリーンベルト・プロジェクトだけで、全ての CTQ について研究することはできないので、AHP や QFD を使って決めた優先順位に基づいて、最も重要な CTQ である温度特性に焦点を当てることにしました。そして Boundary Diagram を使って、装置のどの箇所の温度を調べるのか、研究の対象と範囲を明らかにしました。
もし予想以上の温度上昇があるとすれば、それはどのような現象として現れるのか、どのようなことが原因でその現象が起こりうるのか、Fish Bone Diagram を使って不具合の事象と根本原因を洗い出しました。さらにその不具合の事象(Failure Modes/故障モード)と根本原因(Noise Factors)を P-Diagram に移し、それらの関係付け行いました。
P-Diagram を Design FMEA に変換し、Design FMEA 上で、影響(Severity)や頻度(Occurrence)、検出可能性(Detectability)を検討しました。さらに危険優先指数(RPN: Risk Priority Number)の高い順から対応策を検討し、設計に反映させました。
顧客要求や設計仕様、設計リスク等を理解した後、やっと新しい装置の設計を行いました。
一通り設計が完了した後、その設計に基づいて、熱計算のための数値モデルを作りました。この数値モデルを使ってモンテカルロ・シュミレーションを行い、新しい装置の熱容量が、目標値にどれだけ収まっているか、Z値と PNC(Probability of Non-Compliance)という値を使って確認しました。
TRIZ が導き出した多次元移行原理をヒントに、装置内のコンポーネントの位置を調整し、Z値が最大(PNC値 が最小)となる最適なレイアウトを見つけました。そして最終的な Z値と PNC値から、 新しい装置の設計は熱的に妥当なものであると判断しました。
6. Verify(確認)フェーズ
Verify フェーズでは以下のツールを使いました。
新しい装置はまだ調査のための設計段階なので、実際の装置はありませんでした。そのため「机上の数値モデル(熱計算)が信用できるのか」ということが問題となりました。
そこで現存する比較的類似した製品(装置)を使って、この数値モデルが実際に使えるものかどうか、検討してみました。行ったことは、類似製品を基に同じ方法を使って熱計算・数値モデルを作り、それと実際の測定値を比較するという統計的分析です。
許容できる測定誤差を基に、サンプルサイズの計算をして、その数の類似製品(装置)を用意しました。同じ条件で装置を運転し、温度データを測定しました。そしてその測定データと数値モデルから得た計算値を統計的に比較しました。行った統計的分析は以下の通りです。
- Normality Test
- Capability Analysis
- Equivalent Test
- Two Sample t-Test
- Linearity Test
...