♦ 解の不安定性には常に注意！
１. 我々の住んでいる空間
次元という言葉は魅力的です。「ステレオでは味わえない5.1チャンネルによる３次元の音」、などといわれると如何（いか）にも素晴らしい現実感のある音響を期待します。フラクタル次元も何やら不思議です。マンデルブローの描く複雑な図形が極めて単純な式から発現し、空間を半端な次元で埋める、となると感激してしまいます。さて、我々の住んでいる空間は３次元です。そこで起こること。例えば、天体の運動や電子と原子核の相互作用などは全て３次元空間の性質で決まっています。つまり、重力や電磁気力の1/r2の力というのは、力の発生源の影響が距離rのところの球面（面積4πr2）に一様に広がり、積分すれば一定値を保っている、というだけの条件で決まっている幾何学的な力なのです。これが一般相対論の発想の元になっているのです。
２. 時間とは？
時間の方はどうなっているのでしょう？時計が動いているから時間がたっているのでしょうか？そうではありません。時間が経過していることは、世の中がより複雑化していく（宇宙が膨張している）、つまり、エントロピーが増大していることと同一なのです。意図的に整理しないという条件を付けた状態で、写真を２枚撮ります。後で見て、乱雑度合いの大きい方が、時間が経過した後の写真といえるのです。
３. 偏微分方程式と差分
空間と時間の絡み合った問題の例として、熱伝導の偏微分方程式を考えましょう。
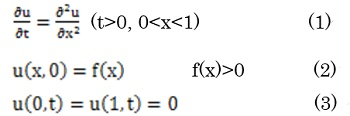
（1）式は１次元の拡散方程式であり、（2）式が時刻t=0で温度分布がf（x）となっているという初期条件、（3）式が両端で時刻によらずに温度一定（0度）の境界条件を表しています。この偏微分方程式を数値的に解いてみましょう。差分の方法は種々ありますが、一番単純で自然な感じのする次式を採用します。
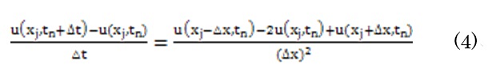
ここで、時間刻みはΔtで、時間はtn+1=tn+Δtと進みます。空間のメッシュサイズはΔxと表しています。
4. 解の安定性
さて、（４）式があれば、後は適当な空間と時間の刻み幅、ΔxとΔtを仮定して、数値計算するだけ・・・のはずです。ところが、適当な値を採るととんでもないことが起こるのです。刻み幅が大きければ計算精度が悪くなるのはしょうがないことですが、そういうレベルの問題ではなく、この例題は、もっと本質的で深刻な問題を含んでいるのです。
例えば、Δx=0.1でΔt=0.01として計算を進めると、uの値が振動を始めるどころか、負の値をとったりするのです。これは、自然現象から考えて不自然です。初期条件として、ある正の温度分布をしていて、両端が0度だったのですから、徐々に全体が冷えていき、０度に近づくだけの時間発展でなければなりません。この問題の場合、r=Δt /（Δx2） が１を超すと解が不安的になることが分かっています。そこで、Δx=0.1にとった場合には、Δt=0.001とかにすれば良いことになります。理由は、時間発展が空間メッシュと関係しているからなのですが、それは（4）式が次のように書き直せることから分かります。この式は、次の時刻での温度は、同じ位置の情報だけではなく、その両隣の値からrという比率で影響を受けることを意味しており、そのため、ΔxとΔt は関係を持つのです。
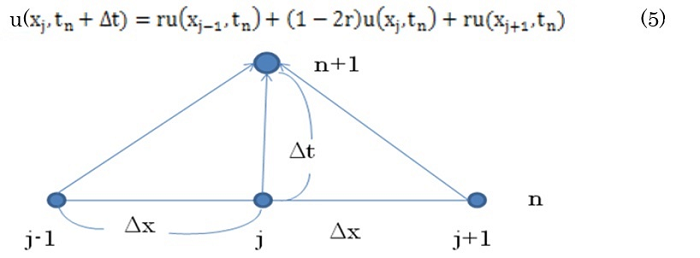
Δtを大きくとっても解が求まる方策も存在します。それは、（4）式ではなく、時間に関して後退微分を用いる方法です。（4）式のように、単純に前の時間ステップの値を使って新しい状態を求める陽解法ではなく、新しい時間ステップの...
このように、空間と時間の刻み幅は、拡散方程式に限らず、時間と空間の関係する方程式を数値的に解く場合に極めて慎重に選ばないといけないのです。上記の例題では、時間発展の様子が最初から直感的に分かるので、解がおかしいかどうかを容易に判断できました。しかし、もっと複雑な条件下での解に対しては、我々の想像力には限度がありますので、現場数学では解の不安定性には常に注意しながら数値計算する必要があります。