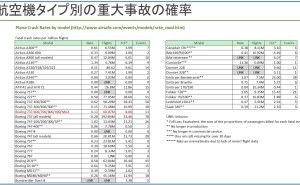
♦ 単なる計算機を使った数値計算の世界ではない
一般的に原理や法則、方程式といいましても、フェルマーの大定理、オームの法則、余弦公式、マックスウェルの方程式……など数も多く、数学や物理の長い歴史を感じます。また、原理・法則・定理・公式・方程式は、それぞれに意味があり、違った名称を与えられているのです。これらは、どれが偉いとかいう問題ではありません。しかし、こういうところに沢山、冠の名前が出てくる人が偉いことは確かです。例えば「数学界の巨人」と呼ばれるレオンハルト・オイラーは群を抜いています。オイラーの公式: eiθ = cosθ + isinθ、オイラーの等式: eiπ + 1 = 0 、オイラーの多面体公式、オイラーの流体力学の方程式、オイラーの剛体回転に対する運動方程式など、みなオイラーが提案したものです。
1. 自然は美しいの意味
世の中の問題を解くための方程式は沢山あります。ラグランジュの運動方程式、シュレディンガー方程式、ラプラス方程式…。これらは、実は、変分原理からオイラーの方程式として導かれるものなのです。変分法というのは、微分が関数の変化を追うのに対して、関数形自体の変化を研究します。つまり、関数を変数とした汎関数の微分です。最初に採り上げられたのは最速降下線の問題でした。この問題は、ある地点A(0,a)から他の地点B(b,0)へ重力によって落ちていく場合に、最短時間で行く経路の形は何かを探すというものです。経過時間をT、y(x)を経路とすると、
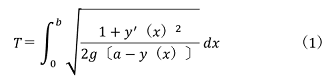
をy(0)=a、y(b)=0の条件下で最小にする関数形y(x)を探すという問題になります。この答えはよく知られているサイクロイドです。ニュートンの運動方程式は、ラグランジュの運動方程式に含まれ、変分原理に基づくものです。つまり、L=T-Vの時間積分(作用)の極値を取る経路が実現される運動になります。単に方程式が経験的に与えられ、それを数値的に解くという一般の人の理解を超え、正しい問題意識を培う必要があります。それが自然を正しく理解する方策なのです。
物理の方程式が成り立つ裏には、必ず何らかの極値問題があり、その汎関数を探す、つまり、最適な「関数形」探索問題が横たわっているのです。これが分かると「自然は美しい」という言葉の本当の意味が理解できますし、品格ある数値計算になり、さらには品質保証の仕方が分かります。経済問題、環境問題、発生生物学の方程式等も、このように考えれば、それら現象の元の何かを最適化するという命題の表現になっているのです。
2. 宇宙レベルで考えると…
数式で表すことで客観的にものごとを表現する、というのが数学のやり方。つまり、不必要な「意味」を削ぎ落として中身だけを記述したのが定理や公式です。それに比べ、法則となると、途端に対象物が決まり、各々の記号が意味を持っています。一見同じようにみえますが、全く別物なのです。物理現象の記述に関しては、統計処理や近似が入るため、完全に一意的に決まる、という訳ではないところも定理や公式とは違います。現場数学では、この違いを良く理解して計算を実行しないといけません。みな同じように見えるので、不必要に計算精度を上げたりしている例が多くみられますが、近似のレベルを超えた精度は元々意味がないのです。
それに比べ、数学の定理や公式は完全に思えます。しかし……話はそんなに単純ではありません。「平行線の錯角は等しい」などという場合には空間が一様であるという想定をしています。当然の様に思われるかも知れませんが、宇宙レベルで考えれば、空間そのものが膨張していたり、平行である2つの線がブラックホールで引き寄せられて変形したりしています。このように、自分の身近で理解できる範囲を拡張して、全宇宙を理解することはできません。さて、宇宙の全てを理解する方程式は何か?実は、宇宙方程式は1915年にアインシュタインが最初に提案したのです。
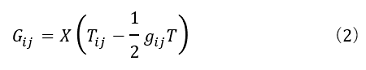
となります。1958年にはハイゼンベルグは原物質の場ψの方程式として別の宇宙方程式を提案しています。これらは、それが解ければ宇宙の全構造が分かるはずである、という壮大な方程式なのです。強い重力場を有するブラックホールや中性子星の問題はこのような方程式を用いて研究されています。もち...