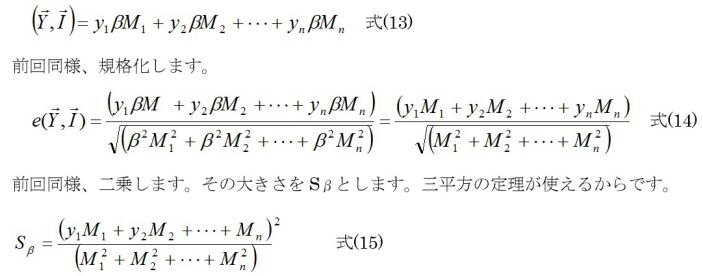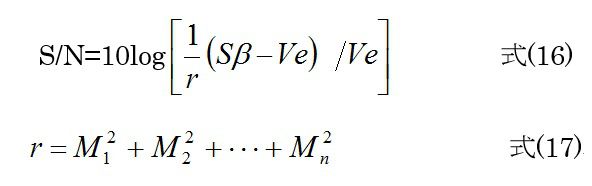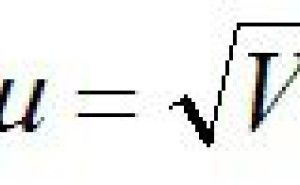代表的なばらつきといえば、Range(範囲)、標準偏差をいいますが、これらは相対的なばらつきではありません。そこで、たとえば標準偏差が1mmと2mmでどちらが大きいかといわれて、前者が平均1cm(10mm)に対するもので、後者が平均10cm(100mm)に対するものであるのなら、前者の方がばらつきが問題になるはずと感じると思います。
頭の中で、前者は1/10=10%, 後者は2/100=2%という計算をしているからです。こういう、スペック中心や平均に対して、どの程度ばらつくのか(通常はその比)を相対ばらつきとよんでいます。有名なものに変動係数があります。これは、CV(Coefficient Variance) と略され、標準偏差を平均で割って表現します。当然、サンプルサイズが異なれば、変わりますが今は考えません。
式で表せば、
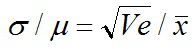
式(1)(右辺は推定値)です。この値は簡易的に
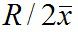
と計算する場合もあります。式(1)を二乗して、分子分母入れ替え、常用対数をとり10倍すれば、品質工学でいう望目特性のSN比に対応します。SN比はよさ加減を表すのでこのように相対ばらつきの逆数にします。
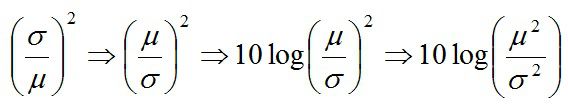
式(2) (デシベルという)
品質工学では、とくにパラメータ設計では制御因子の水準を大きくとって、設計の良否を判定しますから、σは平均レベルに対するもので考えないと意味がないことからも理解しやすい式です。対数をとるのは、加法性を高めるためです。パラメータ設計は、通常設計・開発段階でつかわれ、特性値が広い範囲にまたがるので、対数をとったほうが一般的に加法性が高まって、効果推定や分散分析モデルになじむと考えればいいです。品質工学のテキストによると、大抵の場合、以下のようにSN比計算を導出しています。n個のデータをy1, y2, ,,, ynとすると、
これが、
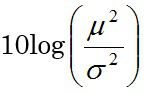
の推定値になっているということでした。しかし、この式は統計学に慣れた人でないとわかりにくいのではないでしょうか。よく、品質工学と統計学は違うという人がいますが、固有技術からすれば同じようなものです。同じ土台はいくらでもあります。統計学がわかっているから、違いも分かるというもので、統計学がわからない人が「違う」といっても説得力ありません。さきほどのSN比算出などは、統計学以外のなにものでもありません。最後に平均の二乗をσの二乗で割るあたりが、統計分布前提でないだけです。
ということは、統計学的にSN比を知っていないとSN比が理解できないこととなり、困ってしまいます。そこで、今回は統計学よりは技術者になじみの深いベクトルの考え方でSN比を説明したいと思います。このほうがピンとくると思います。途中までですが。
まず、特性値はY=(y1, y2, ,,,,, yn)とします。横に並べただけの行ベクトルです。理想特性ベクトルは、平均値mとすると、I=(m, m, ,,, m) とmがn個ならんだ行ベクトルとなります。すべての特性値yが全てmに等しいことが理想と考えるのです。望目特性の場合です。すると、Yの理想方向ベクトル成分はYとIの内積になりますから、その成分は、
St=Sm+Se 式(11)(三平方の定理です。全変動を理想方向ベクトルと誤差ベクトルに分けることができます。二乗するのは、この定理を利用したいからと考えるのです。)Stは、特性の行ベクトルの大きさの二乗和ですから、式(3)と一致します。以降は式(5)、(6)、(7)と同じです。
又、SN比が相対ばらつきの逆数になっている点についてはよさ加減への変換だと考えればいいのですが、なにを良さとしているかについては、単に平均を良さとしていることです。目標値に対してではありません。注意が必要です。いくらSN比が高くなる条件が見つかっても目標が理想方向である平均から遠い場合には、目標値への調整が必要です。そういう意味で、理想方向とかいう場合の「理想」ということばは適切でないかもしれません。
同様のことを、理想特性が「y=βM」(比例式動特性)の場合で考えてみます。Mは信号因子と呼ばれています。今は、この信号Mに対してn個(n水準)で考えましょう。このベクトルは、M=(M1, M2, ,,, Mn) 式(12) と表します。特性値yを前望目特性時と同じく、Y=(y1, y2, ,,,, yn)とします。理想特性ベクトルは、I=(βM1, βM2,,, βMn)ですから、Yの理想方向特性ベクトルは、
ここから先は、ベクトルとは関係なくなって、どこのテキストにも書いてある通りの式になっていきます。式(7)のSmをSβに変えて、動特性比例式の場合のSN比は、下記のようになります。
ところで、この式は
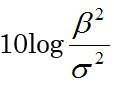
に対応していますが、逆数を相対ばらつきのときと同じように考えれば、βの大きさに対する直線からのズレの大きさとなっています。それを逆数化したものです。二乗したり、対数をとっている理由は前述と同じです。要は、傾きが大きいとそれなりにズレは大きくなるから、傾きで補正してやらないと正当な評価にならないということです。又、σは特性値yの標準偏差ではないことに注意です。さらに、式(16)をdbとよんでいますが、一目瞭然、間違いです。望目特性と違い、動特性のSN比は単位が残ります...
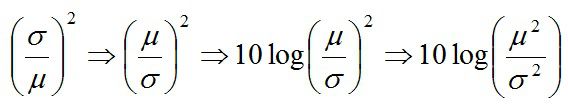 式(2) (デシベルという)
式(2) (デシベルという)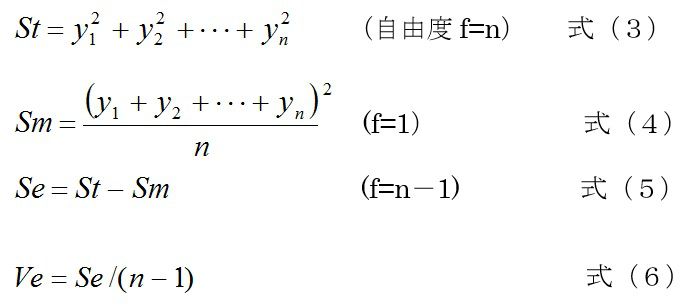
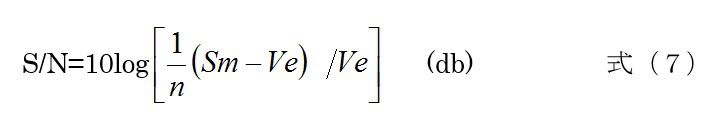
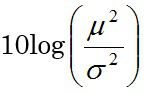 の推定値になっているということでした。しかし、この式は統計学に慣れた人でないとわかりにくいのではないでしょうか。よく、品質工学と統計学は違うという人がいますが、固有技術からすれば同じようなものです。同じ土台はいくらでもあります。統計学がわかっているから、違いも分かるというもので、統計学がわからない人が「違う」といっても説得力ありません。さきほどのSN比算出などは、統計学以外のなにものでもありません。最後に平均の二乗をσの二乗で割るあたりが、統計分布前提でないだけです。
の推定値になっているということでした。しかし、この式は統計学に慣れた人でないとわかりにくいのではないでしょうか。よく、品質工学と統計学は違うという人がいますが、固有技術からすれば同じようなものです。同じ土台はいくらでもあります。統計学がわかっているから、違いも分かるというもので、統計学がわからない人が「違う」といっても説得力ありません。さきほどのSN比算出などは、統計学以外のなにものでもありません。最後に平均の二乗をσの二乗で割るあたりが、統計分布前提でないだけです。