19．実用技術としてのパターン認識
MTシステムの考え方の説明のために、家庭の幸福度やモナリザを例にしてきましたが、ここから実用技術としてのパターン認識について話を進めます。
これまでのご説明でご理解いただけたかと思いますが、MTシステムは次の手順によるパターン認識の手段です。
(1) 一様な集団を集める
(2) 一様な集団の内部構造を相対関係を中心に調べて、集団からの距離をM博士の数理を用いて求める
20．規則性を考える指標：相対関係
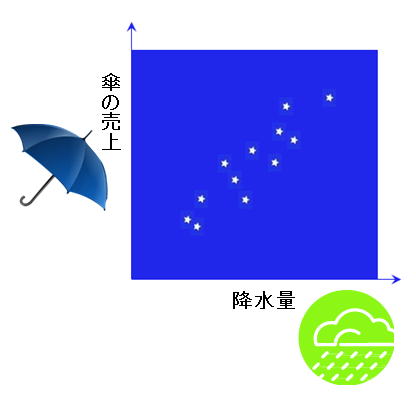
「福笑いの原理＝相対関係の原理」について、月ごとの降水量と傘の売上の例を用いて説明します。
図の横軸は東京都の10年間の各月の平均降水量、縦軸はある店の傘の売上数です。明らかに両者には相対関係があります。雨の多い月は傘がよく売れています。逆に言えば、降水量が多いのに傘が売れなかったとすると、なにか特別なことが起きた可能性があることになります。
いつもの相対関係から外れることはめったにありません。「めったにない程度」を一つの指標で示すことができれば、「パターンの違い」を測れることになります。
降水量と傘の関係は1組の関係ですが、実際の問題では計測値の数はとても多くなります。相対関係を調べる組み合わせもどんどん増えます。しかし、一組の相対関係のことを理解できていれば、あとは同じ規則が増えるだけです。
重要なことは、普通の状態をゼロ点にしておくことです。そして、「普通ではない状態」は相対関係からのズレとして数値化できるということです。M博士の数理を使えば、計測値の数が多くても、そのズレをうまく数値化してくれます。
21．普通からのズレが「おや？」を感じさせる
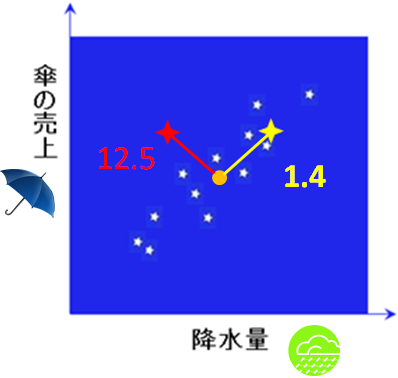
私たちは普通ではないことが起こると、「おや？」と感じます。雨が少ない月に傘の売上が多いときなどです。この「おや？」と数値の関係を以下に示します。
降水量と傘の例の図には、いつもの12個の点とは別の新規データも描きました。これらはそれぞれ、ある月のデータです。「M博士の数理」を使うと黄十字の距離は1.4になります。しかし赤十字の距離は12.5になります。赤十字は、いつもの点群すなわち「普通の状態」とは異なっていることが数値からわかったということになります。
橙色の丸点は、12個の点群の重心位置です。つまり、降雨量と傘売上の各平均値です。ここが距離ゼロの位置になります。この点から黄と赤十字の点までの距離は、定規で測ればほぼ同じです。しかし、M博士の数理を使えば「相対関係を考慮した」距離になります。 M博士の距離が、例えば4以上になったら、コンピュータに「おや？」と言ってもらえばよいことになります。
22．相対関係を楕円で表す
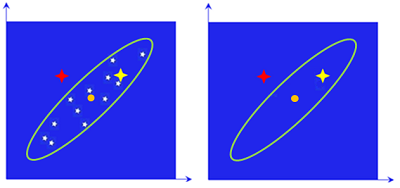
12個の点群がほぼ全部収まるような楕円を描くことができます。白い星を消したのが右側の図です。こうすると、黄と赤のマークの距離の意味が分かります。12個の点は共通の規則性を持つ集団であり、その規則性が楕円で代表されています。
ある大きさで描いた楕円の中にある点（黄）は、その規則性を維持した「仲間」であり、M博士の距離（M距離）は小さい値になります。外にある点（赤）は仲間ではなく、M距離は大きな値になります。
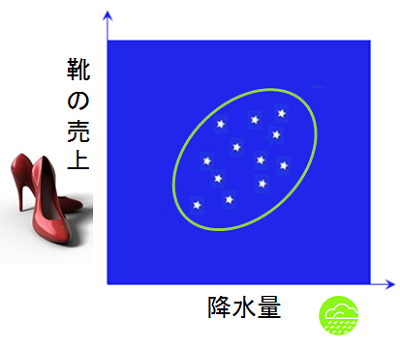次に降雨量と、ある店の「靴の売上」について点群を描きました。雨が多いと若干は靴の売上が増えるようですが、それほど大きな相対関係（これからは「相関」と呼びます）はありません。靴は季節の節目にたくさん売れるようです。
この点群に同じように楕円を描きました。楕円は、傘のときより円に近くなっています。このように、相関の程度は楕円の形状で表現することができます。楕円が細いほど、相関が高いことになります。
23．項目が5つあるとき
降雨量と傘の売上だけの関係を見るなら、相関は1組だけでした。しかし、考慮すべき項目の数によって組み合わせ数は増えます。
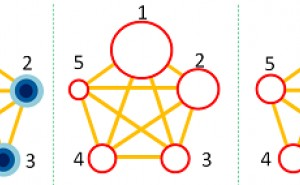
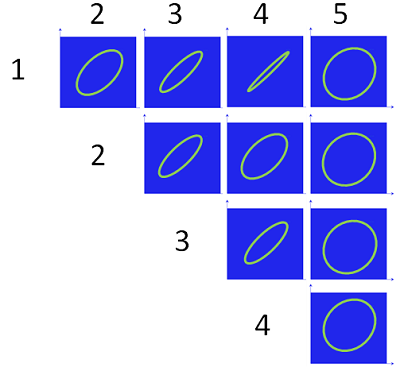例として、考慮すべき項目が5つあるときにはどうなるでしょう。組み合わせの数は図の橙色の線の数だけあります。つまり、10組です。そして、組み合わせごとに相関があります。
それぞれの組み合わせごとに「相関...
