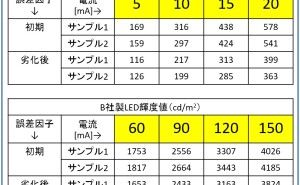
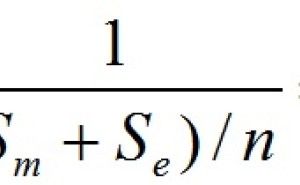2.5. 従来のSN比の課題(4) ~計算の複雑さ(使用面、教育面での困難性)~
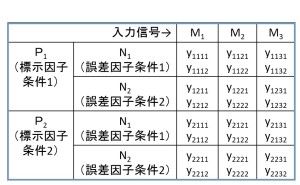
たとえば動特性のSN比の場合、偶然誤差の変動Veを計算する必要があります。そのため、交互作用項を含めた複雑な分解計算が必要です。また自由度の理解も必須となります。図2.5.1のような、標示因子P、ノイズ因子N、信号因子M、繰り返しがある場合のデータの場合、以下の要因の変動をすべて計算してVeを求める必要があります(カッコ内は自由度)。交互作用は残差にプールできるものも多いのですが、そのためには分散分析が必要で、いずれにしても多数の変動への分解は必要です。
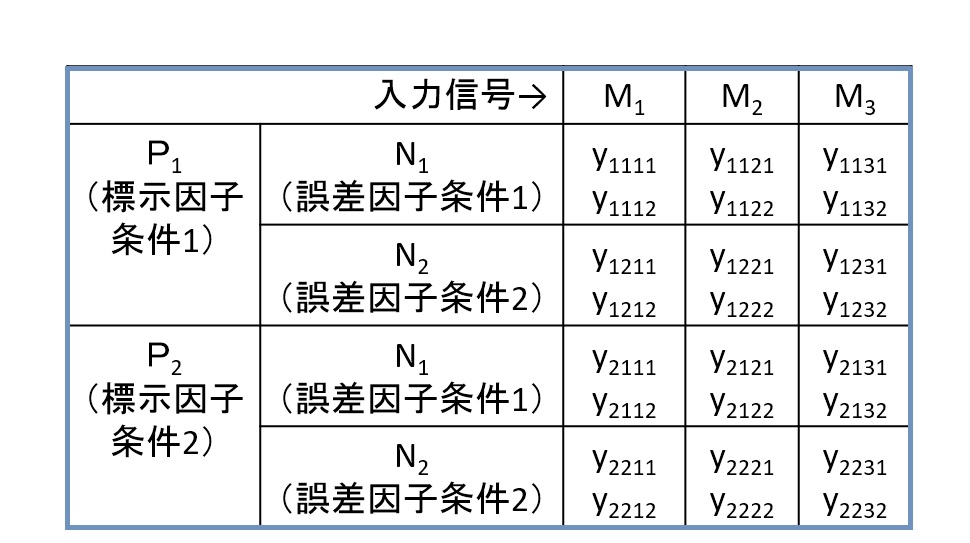
図2.5.1 標示因子・信号因子・誤差因子・繰り返しを含むデータモデル
全変動:T(24)
主効果:β(1), P(1), N(1), M(2)
2因子交互作用:β×P(1), β×N(1), β×M(2), P×N(1), P×M(2), N×M(2)
3因子交互作用:β×P×N(1), β×P×M(2),
β×N×M(2), P×N×M(2)
残差:e(3)
以下、エネルギー比型SN比について従来のSN比との比較で議論しますが、SN比の違いにかかわらず、SN比計算で使用するデータ(機能の定義:何を計測するか、ノイズ因子の定義:どのような有害要因に対する評価なのか)の質が重要です。しかし本稿ではそれは前提条件として成り立っているものとします。つまり技術的には正しい機能、ノイズ因子を用いているのに、計算方法によって、結果に違いが表れる場合を議論します。
3. エネルギー比型SN比
2008年に筆者を含めた関西品質工学研究会の研究グループが提言したエネルギー比型SN比は、技術評価における新しいSN比です。機能の出力における「有効エネルギーSβ(目的に使用された成分)」と「有害エネルギーSN(目的外に使用された有害な成分)、必要に応じて「無効エネルギーS0(有効でも有害でもない無効成分、標示因子の変動)」に分解して、SβとSNの比をエネルギー比型SN比と定義しました。
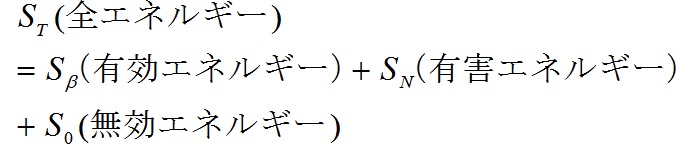
式 3.0.1
ここでの「エネルギー」は広義にとらえており、出力の2乗の量(2乗和)を指しています。したがって、機能の出力をエネルギーの平方根(1/2乗)の単位にとると、2乗和がエネルギーに相当することになり、2乗和の分解が数学的に成立するだけでなく、「物理的にも」成立しやすくなります。そこで、エネルギー比型SN比をηEで表すと、式3.0.2のように非常に簡明な形になります。
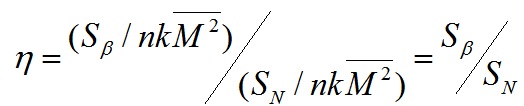
式 3.0.2
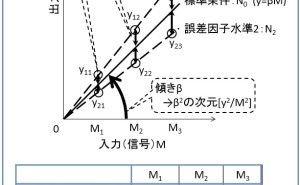
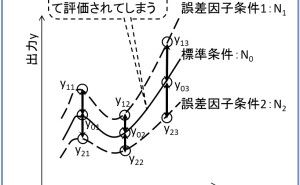
従来のSN比と形が似ていますが、これは「基準化した誤差成分の逆数」という観点ではなく、「目的に使用された有効成分と、目的外に使用された有害成分の比」という技術的な観点を明確にしたSN比です。ηEでは自由度の計算も、Veの計算も不要です。分母のSNは主にノイズ因子による影響の成分SN×βですが、さらに偶然誤差Seを含めてもよいでしょう(そのほうが、総合評価になるし、後述のように計算がより簡単です)。エネルギー比型SN比は、技術者が考える能動的なノイズ因子(統計的な偶然誤差でないことに注意)を導入して、その水準の端と端の差をそのまま変動と認めて記述するという考え方をとります。簡単のためn=2水準の場合、エネルギー比型SN比の分子(有効エネルギー成分)は、式3.0.3です。
![]()
式3.0.3
これは平均の傾きβN0の2乗である。一方、分母(有害エネルギー成分)は主に、能動的なノイズ因子の影響の成分SN×βであり、式3.0.4です。
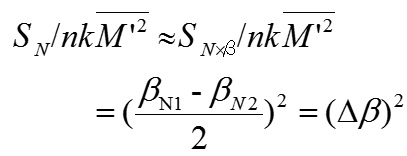
式3.0.4
これは、平均の傾きβN0からの変化量Δβの2乗で...