前回の【快年童子の豆鉄砲】(その93)MD解析法による適材適所配属(1)に続けて解説します。
2.適材適所配属のためのMD解析法の使い方
4)MD解析法活用ステップ
これ以降、事例1のデータを使って、MD解析法の具体的な活用ステップをご説明します。
Step 1:解析対象データの採取
“採取”とありますが、MD解析法の場合、この事例のように、複雑な事象(新入社員)を理解しようと、多くの特性について調査して手に入れた「特性(変数)×サンプル」のマトリックス・データ(MD)の取り扱いに苦慮し、その解決策としてMD解析法を活用しようというケースが多く、その場合は、このステップは不要となります。ただ、新しいテーマに取り組む場合や、後述する事例2のように、既存データがカバーしきれていない特性がある場合には、その目的に合った新たなデータの採取が必要になります。その場合、下記2点がポイントになります。
【ポイント1】特性は極力幅広く採用する
データ採取に当たっては、解析対象が複雑で全貌を把握できていない状況ですので、測定対象は、先入観による特性排除は避け、むしろ気になる特性があれば採用しておき、取捨選択は、解析結果を見て行います。
【ポイント2】サンプル数は20以上がめど
サンプル数は母集団の推定精度と経済性の兼ね合いで決めることになるのですが、めどとしては、推定精度をサンプル数の大きさに頼る“大標本法”と、少ないサンプルでt変数を用いて推定する“小標本法”との誤差がほとんど無視できるサンプル数といわれる20以上が妥当と思われます。ただし、変数の数を下回ったのでは解析の意味がなくなりますので要注意です。この事例の場合はサンプル数が39ありますので問題ないといえます。ただ、「多変量解析法」(奥野忠一他著、日科技連出版、P.220)に、サンプル数50のモデル実験結果が出ているのですが、大筋で傾向は変わらないものの、各統計量は真の値とはかなり異なっています。既存データを使う場合、サンプル数は自由にならないことが多いだけに、解析結果に対する判断を下す時、サンプル数が50くらいあってもこの程度であるということを念頭においておく必要があります。
Step 2 : データの背景確認
新たに解析用データを採取する場合は解析目的に合わせることができるのですが、この事例のように、既存データに頼らざるを得ないケースの場合、データ採取の背景を把握しておいて、解析結果の判断に反映するなどの配慮を心がける必要があります。この事例の場合、データの採取背景については、公的にオーソライズされた、当時の労働省編「職業適性検査結果」9項目に加えて、工場独自の筆記試験結果も採用されていますので当時としては申し分ないと言えます。
Step 3 : データの入力
解析の起点ですので、入力ミスに最大限の注意を払う必要があります。入力ミスのチェックは、入力した変数ごとの平均値と原本の平均値と照合するのが効率良く確実です。この事例の場合、平均値が合わない特性があり、チェックしたところ2か所の入力ミスが見つかっています。
このケースでは、解析結果に影響するような入力ミスではなかったのですが、解析結果に対する違和感からの原因調査段階で入力ミスによるものと分かった場合は、それまでの解析努力が無駄になりますし、一番恐ろしいのは、解析結果に大きな影響を与えるような入力ミスに気付かず、その解析結果をもとに誤った諸判断を下してしまう場合です。このようなリスクを避ける意味で、入力ミスチェックは確実に実施する必要があります。
Step 4 : 解析対象データの正規性の確認
統計解析は、母集団が正規分布していることを前提としていますので、解析対象母集団が正規分布とみなせるかどうかの確認は大切で、どのように確認するかをご説明します。そのために、上記データから平均値・標準偏差・歪度(わいど)・尖度(せんど)の基本統計量を求めます。
母集団の分布の正規性確認は、この後の解析と解析結果に対する判断の死命を制することですので、これらの数値は、解析ソフトで一括して出てくるのですが、解析を人に頼む場合でも、ここまでは解析責任者が自分自身でチェックし、その後の解析努力に値するものであることを確認しておくべきと言えます。
【ポイント1】データ吟味の際のめど
平均値と標準偏差は、データの全貌把握手段として通常の取り扱いで良いのですが、歪度と尖度については下記を参考に判断していただければと思います。
“歪度(skewness)”と“尖度(kurtosis)”について
“歪度”は、“ひずみ”とか“ゆがみ”とも言われ、分布の非対称性を示す指標で、Z値(データと平均値の差を標準偏差で割った値)の3乗の平均値で、正規分布の時はゼロとなり左右対称を、負の値を取るとき分布の山の右への偏りを、正の値の時は左への偏りを示します。
“尖度”は、“とがり”とも言われ、Z値の4乗の平均値から3を引いた値で、分布のとがり具合(分布の裾の広がり具合)を示し、正規分布の時はゼロ、正の値の時は裾が正規分布より広がった形状、負の値の時は、裾が短くとがった形状になります。3を引くのは、分布の特徴を論ずるとき、正規分布の時に両者とも“0”にするためで、3を引かないケースもあるので要注意です。
通常“歪度”は“-0.7~0.9”、“尖度”は“‐0.4~0.8” とされていますが、双方とも目安として、絶対値が“1.5”を超えたら、データに異常値が含まれている可能性が高いと判断し、ヒストグラムを書くなどして分布の状況をチェックし、明らかに解析結果を目的に反して乱すと判断されるデータについては修正するなど適正な処置をとる必要があります。ただ、分布上特異なデータが、解析結果を示唆に富む画期的な結論に導くケースがありますので、杓子定規に安易な削除や修正は慎み、異常値の背景を把握して、解析結果に対する判断に反映するのが無難と言えます。
事例の基本統計量は表76-1に示す通りで、絶対値が1.5を超える場合は太字にしてあります。
表76-1 基本統計量
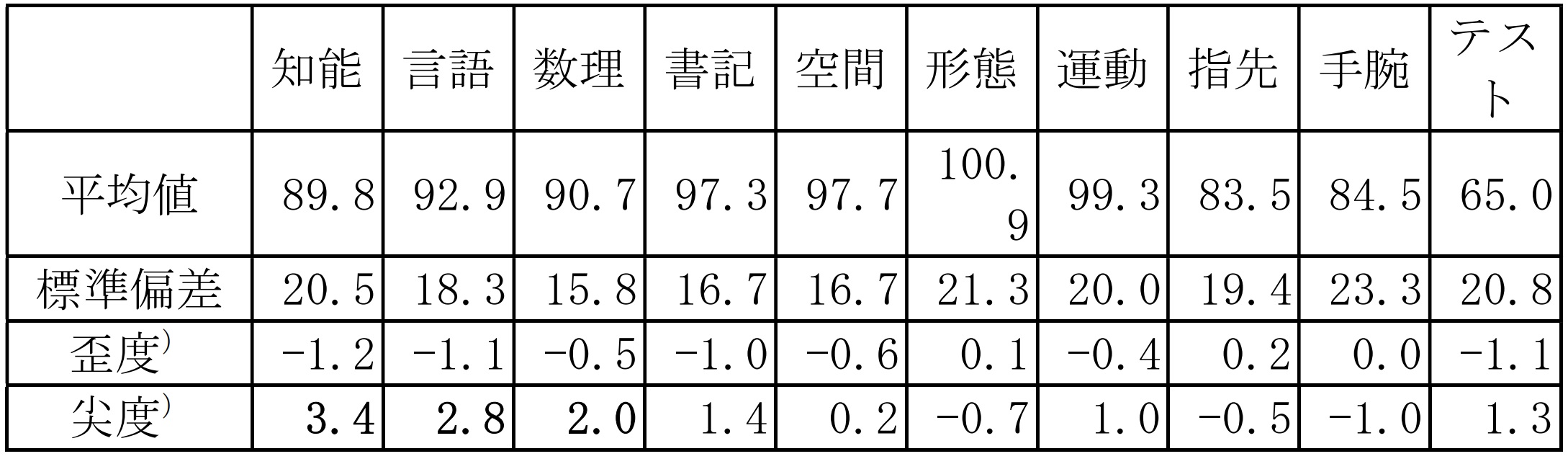
上表を基にデータを吟味したところ、知能、言語、数理に関し“尖度”の値が正規性に対する懸念点である“1.5”を超えているのでヒストグラムを描いてみた結果を図76-1に示しています。

図76-1 「知能」「言語」「数理」のヒストグラムと推定分布形状(点線)
...