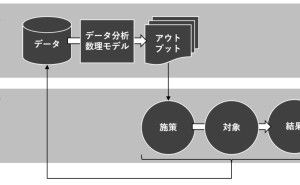
◆ 結局のところ、ビジネスデータ分析は因果関係を知りたい
ここ数年、統計学系のモデルよりも機械学習系のモデルに注目が集まっているように感じられます。どちらが良くてどちらが悪いというわけではありませんが、向き不向きがあるようです。
単に「当てる」というだけなら、機械学習系のモデルのほうに分がありそうです。一方で、「何がどうなっている」ということを知りたいなら、統計学系のモデルのほうが分がありそうです。ビジネス系のデータ分析は、どちらのほうが性に合っているのでしょうか?
今回は、「結局のところ、ビジネスデータ分析は因果関係を知りたい」というお話しをいたします。
1. 1変量の分析から2変量の分析へ
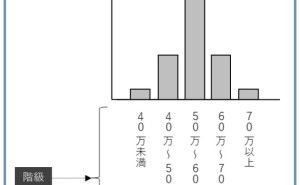
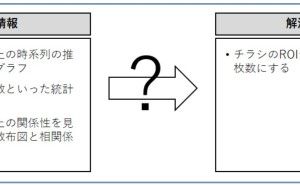
多くの人は、手元にデータがあれば、初めの作業はグラフ化したり散布図で確認するのかと思います。データの時系列の遷移を折れ線グラフで表現したり、データのばらつきを見るためにヒストグラムと呼ばれる棒グラフで表現したりします。ここまでは、あくまでも1変量データのお話しです。1変量データとは、文字通り変数が1つの量的なデータという意味です。
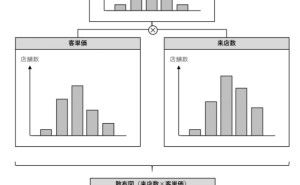
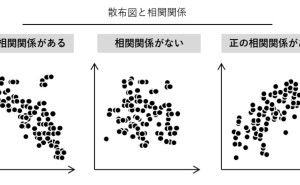
2変量になると、多くの人は散布図というものを描きます。2変量というぐらいなので、量的な変数が2つあるデータです。例えば、小売店であれば「来店客数」と「売上」は2変量データです。「来店客数」と「売上」を1日単位で集計し、横軸に「来店客数」、縦軸に「売上」とした散布図を描けば「来店客数」と「売上」の関係性が見えてきます。想像通り「来店客数」が増えるほど「売上」が増えるという関係が見えてきます。いわゆる相関関係です。
2. データが手元にあれば、とりあえず相関分析
量的なデータは、通常2つだけではありません。たくさんあります。
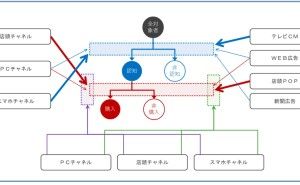
小売店の例でちょっと考えただけでも「客単価」や「気温」、「降水量」、「値引き率」、「チラシの配布枚数」などです。さらに、カテゴリー別や商品別に「売上」や「粗利」、「単価」、「売上点数」など量的データを分けることもできます。広告宣伝・販促施策ごとの量的データを考えれば「テレビCM」や「新聞広告」、「交通広告」、「リスティング広告」などもありますし、それをエリア・店舗ごとに細かく設定することもできます。
つまり、2変量の組み合わせが多く存在しますが、それらすべての散布図を描き確認するのは大変です。この散布図の相関関係を、1つの数字で表せないものかと誰もが思います。1つの数字で表したのが相関係数です。
相関係数は「-1~+1」の間の数値をとり、「0」の値いに近いほど相関がなく「+1」の値に近いほど正の相関があり「-1」の値に近いほど負の相関があるといいます。「来店客数」が増えるほど「売上」が増えるという関係は、正の相関です。このことから、売上を増やすには来店客数を増やせばよい、ということが見えてきます。「降水量」が増えるほど「来店客数」が減るという関係は、負の相関です。このことから、雨が多く降ると来店客数が減るな、ということが見えてきます。
総合すると「雨がたくさん降ると来店客数が減り、来店客数が減るので売上が減る」ということが見えてきます。このことから、相関分析から因果関係を見ることができるのです。
そして多くの場合、相関分析をすることで因果関係を知りたいと思っているのではないでしょうか。結局のところ、ビジネスデータ分析で因果関係を知りたい、というのが本当のところだと思います。因果関係が分かることで、問題の要因探しに役立ちますし、次の打ち手にも繋がります。後ほどお話しする回帰モデルを構築すれば、未来を予測したりシミュレーションするのにも役立つからです。
3. ビジネスデータの多くは、時系列データ
ビジネスデータの多くには、「時間概念」が付随します。
例えば、昨年1年間の売上であれば「昨年」という「時間概念」が付随していますし、先月の来店客数であれば「先月」という「時間概念」が付随します。時間概念が付随するデータの多くは、先ほども少し触れましたが多くの場合、時系列推移を折れ線グラフで表現し、どのように推移しているのか確かめるかと思います。
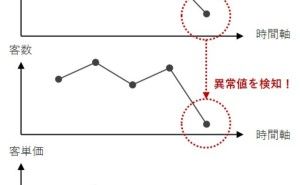
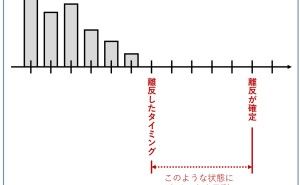
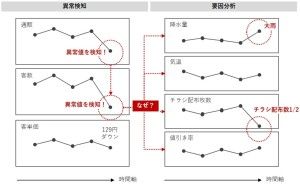
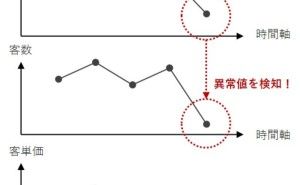
日別の売上の折れ線グラフの推移を見ると、一直線の折れ線グラフではなく、小さく上下に振動していたり、ある時期に上昇していたり、逆に下降したり、または緩やかに上下するサイクルがあったりと、規則性と不規則性が同居しているかと思います。
この動き方が何に起因するのか、それが大きな問題です。
流行り廃れを反映したものなのか、季節性(春・夏・秋・冬)を反映したものなのか、天候(気温や降水量など)によるものなのか、誤差的なものなのか、それとも広告宣伝・販促施策の影響なのか、など様々な要因が考えられます。このようなデータに対し、散布図を描くとどうなるでしょうか?
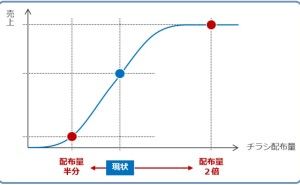
例えば、「売上」と「チラシの配布枚数」。
恐らく、正の相関(相関係数の値がプラス)があり、「チラシの配布枚数」が増えるほど「売上」は増えるということが分かることでしょう。この相関係数は、どこまで正しいのでしょうか。「売上」には季節性や天候(気温や降水量など)の影響などが混じっています。要するに、季節性や天候などの影響が混在した「売上」と「チラシ尾配布枚数」の相関係数なのです。
つまり、「売上」と「チラシの配布枚数」の相関係数にはやや問題があり、純粋に「売上」と「チラシの配布枚数」の関係性を反映していません。そう考えると、この相関分析からみた因果関係に対し、少し不安を覚えることでしょう。
4. 回帰分析という視点から考えてみる
相関分析に近しい分析に、回帰分析というものがあります。
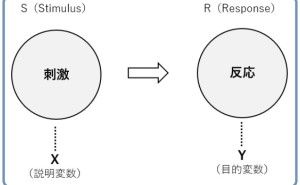
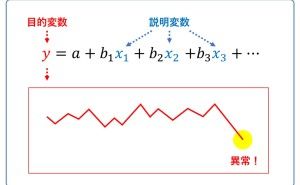
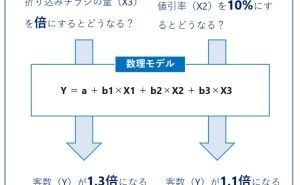
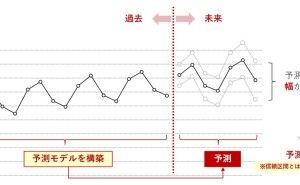
回帰分析は、一方を「目的変数」、他方を「説明変数」として、その関係性を1つの数式(回帰モデル式)で表すぐらいです。1つの数式(回帰モデル式)で表すため、予測などで利用することができます。「説明変数」に何かしら数値を代入すると「目的変数」の予測値を求めることができるからです。
先ほどの例でお話しすると「目的変数」を「売上」とし、「説明変数」を「チラシの配布枚数」とすると「チラシの配布枚数」で「売上」を予測する「回帰モデル式」で表すことになります。
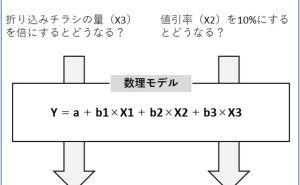
相関係数に相当するものとして、回帰係数というものがあり「回帰モデル式」の説明変数に対する係数になります。簡単に数式で表現すると以下のようになります。
「売上」= 定数項 + 回帰係数 ×「チラシの配布枚数」
この回帰係数と相関係数は連動しています。先ほど「売上」と「チラシの配布枚数」の相関係数にはやや問題があり、純粋に「売上」と「チラシの配布枚数」の関係性を反映していないというお話しをしました。この問題は、相関分析だけでなく回帰分析でも同様の問題となります。つまり、因果関係を知るためには相関分析や回帰分析は非常に有効ですが、時系列データの場合にはやっかいだということです。
5. SARIMAXという解決策
季節性や天候などの影響が混じった「売上」ではなく、季節性や天候などの影響を取り除いた「売上」との「チラシの配布枚数」との関係性を知りたい…。このようなことはできるのでしょうか。
解決策の1つとして、SARIMAXという統計学系のモデルがあります。SARIMAXモデルと呼ばずに、ARIMAモデルと呼ぶ場合が多いですが、正確にはSARIMAXといいます。日販(1日の売上)で考えれば、ARIMAモデルは、週単位や月単位、季節単位の売上の短期的なサイクルを表現し、さらに上昇傾向や下降傾向ということも表現します。
さらに、SARIMAXの「S」は「Seasonal」を意味し、長期的なサイクル(年単位など)に加え、上昇・下降傾向などを表現します。SARIMAXの「S+ARIMA」で、売上自身のこのような特徴を表すことができます。
さらにさらに、SARIMAXの「X」で売上自身ではなく「降水量」などの影響を反映させることができます。
このSARIMAXの「X」は、回帰分析でいうところの「説明変数」になります。この「説明変数」部分の「X」の1つとして「チラシの配布枚数」を指定します。要するに、SARIMAXでモデル化すれば、季節性や天候などの影響を取り除いた「売上」と「チラ...